ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

Динамическое программирование - один из разделов математического программирования, в котором процесс решения может быть разбит на отдельные этапы (шаги). Это разбиение осуществляется по различным принципам. В некоторых задачах по временным периодам, в других - по объектам управления. Иногда разбиение производится искусственно.

Такой подход позволяет свести одну большую по размерности задачу ко многим задачам, имеющим меньшую размерность. Это значительно сокращает объем вычислений и ускоряет процесс принятия управленческих решений.

Модели динамического программирования применяются для решения экономических задач следующих типичных областей:

- разработка правил управления запасами, устанавливающих момент пополнения запасов и размер пополняющего заказа;

- разработка принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию;

- составление календарных планов текущего и капитального ремонта сложного оборудования;

- выбор методов проведения рекламной кампании, знакомящей покупателя с продукцией фирмы;

- систематизация методов поиска ресурсов ценного вида.

Основные принципы динамического программирования рассматриваются на следующих примерах.

Задача определения пути

наименьшей стоимости

Мистер М. решил отправиться в путешествие из пункта 1 в пункт 10 на дилижансе. В бюро путешествий ему показали карту с нанесенной на ней схемой маршрутов движения дилижансов (см. рисунок).

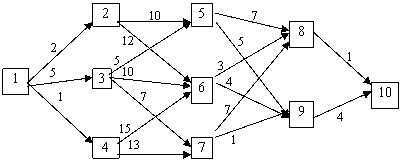
Каждый квадрат на схеме изображает один из населенных пунктов, которые для удобства пронумерованы. Стоимость переезда из пункта i в пункт j обозначим через с_ij (значения этих величин для рассматриваемого примера отмечены на схеме).

Требуется определить такой путь из пункта 1 в пункт 10, общая стоимость которого является минимальной.

Заметим, что формально данная задача может быть представлена в виде математической модели задачи комбинаторного программирования, однако ее особенности позволяют построить следующий алгоритм решения.

Прежде всего отметим, что любой путь движения из пункта 1 в пункт 10 включает четыре дилижансовых маршрута (или четыре «шага»).

Далее важно сформировать следующий принцип.

Принцип оптимальности Беллмана

Каким бы ни был путь достижения некоторого пункта, последующие решения должны принадлежать оптимальной стратегии для части пути, начинающейся с этого пункта.

Таким образом, например, оптимальный путь из пункта 6 не зависит от того, каким образом путешественник в него прибыл.

Для использования принципа оптимальности введем следующие обозначения:

- стоимость, отвечающая стратегии минимальных затрат для пути от пункта i, если до конечного пункта остается n шагов;

- решение, позволяющее достичь .

Здесь индекс n не только равен количеству шагов, оставшихся до конечного пункта, но и совпадает с номером этапа в процессе решения задачи. Таким образом, начинаем поиск оптимального маршрута от конечного пункта, положив n=1.

, ;

, .

n=2

;

;

.

Определены оптимальные маршруты из пунктов 5, 6, 7 (см. рисунок), от каждого из которых до конечного пункта два шага. На следующем этапе используем эти результаты.

n=3

;

;

.

Теперь известны оптимальные затраты и маршруты для пунктов 2,3,4. Осталось рассмотреть последний этап.

n=4

Таким образом, определен оптимальный путь: 1-3-7-9-10, затраты по которому составляют .

Обобщая данный процесс, получаем формулу:

где N- количество этапов в решении.

Определение 1. Данная формула называется рекуррентным соотношением Беллмана. Алгоритм, основанный на применении этой формулы, называется рекуррентным алгоритмом. Подобные алгоритмы являются основным методом динамического программирования.