Динамические
модели.
Магистральная
модель Дж. фон Неймана
Рассмотренные выше модели МОБ были статическими, т.
е. относились к какому-то одному периоду времени. Динамическая модель отражает развитие
экономической системы во времени и отличается от статической следующими
чертами:
- содержит соотношения, определяющие зависимость
последующих состояний от предыдущих;
- предусматривает дифференциацию конечного продукта
каждого периода на две составляющие - непроизводственное потребление и
накопление (инвестиции).
Существуют различные типы динамических моделей.
Все они довольно сложны и различаются в основном по способу описания
взаимосвязи инвестиций с динамикой объемов производства.
Особую группу составляют магистральные
модели. Они позволяют рассчитывать оптимальные траектории экономического роста
(магистрали). Критерии оптимальности, а также предпосылки и допущения, при
которых формулируются модели, могут быть разными.
Рассмотрим магистральную модель равновесного
роста, предложенную американским математиком Дж. фон Нейманом. Она
называется равновесной потому, что моделирует процесс развития экономики в
предположении, что пропорции потребления и инвестиций постоянны.
Будем рассматривать развитие
экономической системы в дискретном времени (по годам).
Для года
можно записать:
![]() , (1)
, (1)
где
![]() - вектор валового производства;
- вектор валового производства;
![]() - соответствующий конечный продукт;
- соответствующий конечный продукт;
![]() - вектор инвестиций;
- вектор инвестиций;
![]() - вектор потребления (выбытием основных фондов пренебрегаем).
- вектор потребления (выбытием основных фондов пренебрегаем).
Пусть известен вектор ![]() , определяющий сложившуюся структуру потребления. Будем
считать его постоянным. Тогда
, определяющий сложившуюся структуру потребления. Будем
считать его постоянным. Тогда
![]() , (2)
, (2)
где
![]() - суммарный конечный продукт.
- суммарный конечный продукт.
Для определения ![]() можно воспользоваться
тем, что суммарный конечный продукт равен суммарной условно-чистой продукции:
можно воспользоваться
тем, что суммарный конечный продукт равен суммарной условно-чистой продукции:
![]() (3)
(3)
где
![]() - вектор относительной
условно-чистой продукции. Его компоненты определяются по уже известной нам
формуле
- вектор относительной
условно-чистой продукции. Его компоненты определяются по уже известной нам
формуле
![]()
Объединяя формулы (2) и (3), получим соотношение,
выражающее потребление как функцию валового производства:
![]() (4)
(4)
где
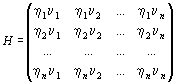 .
.
Рассмотрим теперь, какова
связь между валовым производством и инвестициями. Очевидно, что инвестиционный
спрос зависит от желаемого прироста валового производства:
![]() (5)
(5)
где К - матрица
коэффициентов капиталоемкости (приростной фондоемкости).
Она характеризует капитальные
затраты, необходимые для наращивания производственного потенциала отраслей. Коэффициент
![]() этой матрицы
показывает, какое количество продукции i-й отрасли необходимо для того,
чтобы за счет наращивания фондов обеспечить единичный прирост производства
в j-й отрасли.
этой матрицы
показывает, какое количество продукции i-й отрасли необходимо для того,
чтобы за счет наращивания фондов обеспечить единичный прирост производства
в j-й отрасли.
Как было сказано выше, в модели предполагается
стабильный, равновесный рост. Если темп роста обозначить через ![]() , то
, то
![]()
Из этого следует, что
![]()
Итак, мы выразили две составляющие конечного
продукта через валовое производство. Подставляя (4) и (5) в формулу (1),
получаем
![]() (6)
(6)
Заметим, что в этой модели индекс времени не играет
никакой роли. Так получилось потому, что модель сформулирована в предположении,
что ситуация в каждом следующем году структурно повторяет ситуацию предыдущего
года.
Опуская индекс времени и осуществляя простейшие
преобразования, из соотношения (6) получаем
![]()
Если предположить, что в матрице приростной
фондоемкости отсутствуют нулевые строки (в общем случае это условие не
выполняется, поскольку не все отрасли производят средства производства), то, умножив обе части последнего
соотношения на K-1, получаем
![]()
где
![]()
Таким образом, расчет параметров равновесного роста
сводится к определению собственных значений
и собственных векторов матрицы ![]() . В нашем случае множество собственных значений есть
множество возможных темпов роста. Очевидно, нас интересует наибольший темп.
Поэтому здесь необходимо решить не общую, а так называемую частную задачу, т.
е. найти наибольшее собственное значение
. В нашем случае множество собственных значений есть
множество возможных темпов роста. Очевидно, нас интересует наибольший темп.
Поэтому здесь необходимо решить не общую, а так называемую частную задачу, т.
е. найти наибольшее собственное значение ![]() и соответствующий ему вектор X.
и соответствующий ему вектор X.
Как известно, собственные векторы находятся с
точностью до постоянного множителя. Можно так подобрать этот множитель, что
сумма компонентов вектора Х будет равна 1. В этом случае мы получим магистраль
фон Неймана - пропорции валового производства, при которых обеспечивается
сложившаяся структура потребления и достигается наибольший ежегодный
экономический рост.
Модель фон Неймана формулируется при жестких
условиях и предположениях, поэтому представляет собой сугубо абстрактное
построение. Тем не менее она имеет важное значение, поскольку дает
теоретическое обоснование того, что одним из условий интенсивного, устойчивого
развития экономики является оптимизация пропорций валового производства.