Модель Леонтьева. Коэффициенты прямых

и полных материальных затрат

Рассмотренная таблица МОБ всего лишь форма представления статистической информации о взаимосвязи отраслей. Перейдем теперь к построению математической модели. Для этого введем понятие коэффициентов прямых материальных затрат:

(1)

Коэффициент a_ij показывает, какое количество i-го продукта затрачивается на производство единицы j-го продукта.

Поскольку продукция измеряется в стоимостных единицах, коэффициенты прямых затрат являются величинами безразмерными. Кроме того, из (1) следует, что

(2)

Считая коэффициенты прямых материальных затрат постоянными, запишем систему балансовых соотношений

следующим образом:

Перенося y_i в правую часть, а x_i в левую и меняя знаки на противоположные, получаем

В матричной форме эта система уравнений выглядит следующим образом:

X - AX = Y или (E - A) X = Y,

где Е - единичная матрица n-го порядка;

- матрица коэффициентов прямых материальных затрат.

Итак, мы получили систему уравнений межотраслевого баланса, которую называют моделью Леонтьева. Используя эту модель, можно ответить на основной вопрос межотраслевого анализа - каким должно быть валовое производство каждой отрасли для того, чтобы экономическая система в целом произвела заданное количество конечной продукции?

Следует отметить одно важное свойство матрицы А - сумма элементов любого ее столбца меньше единицы:

(3)

Для доказательства разделим обе части балансового соотношения

на х_j и, выполнив простейшие преобразования, получим

где v_j / x_j= - доля условно-чистой продукции в единице валового выпуска.

Очевидно, что >0, так как в процессе производства не может не создаваться новой стоимости. Из этого следует справедливость соотношения (3).

Свойства (2) и (3) матрицы А играют ключевую роль в доказательстве ее продуктивности, т. е. в доказательстве того, что при любом неотрицательном Y система

X - AX = Y или (E - A) X = Y,

имеет единственное и неотрицательное решение Х=(Е-А)^-1Y. Матрицу (Е-А)^-1 обозначают через В и называют матрицей коэффициентов полных материальных затрат, или обратной матрицей Леонтьева. Коэффициент b_ij этой матрицы показывает, каким должен быть валовой выпуск i-й отрасли для того, чтобы обеспечить производство единицы конечного продукта j-й отрасли. Используя матрицу В, можем записать

Х = ВY

или в развернутом виде

Преимущество такой формы записи балансовой модели состоит в том, что, вычислив матрицу В лишь однажды, мы можем многократно использовать ее для вычисления Х прямым счетом, т.е. умножением В на Y. Это гораздо проще, чем каждый раз решать систему линейных уравнений.

Обратную матрицу В можно вычислить, используя метод обращения с применением формулы разложения ее в матричный ряд:

В=Е+А+А²+...+А^k+... (4)

Число членов ряда, необходимое для получения достаточно точного приближения, зависит от матрицы А, но в любом случае приемлемый результат достигается при k³ 30.

Формула (4) имеет строгое математическое доказательство. Но мы ограничимся тем, что попытаемся осмыслить ее, рассматривая Х как результат некоторого гипотетического процесса последовательного уточнения промежуточной продукции, необходимой для создания заданного конечного продукта.

Итак, вектор конечной продукции, которую должна произвести экономическая система, равен Y. Будем считать, что это и есть первоначальное задание отраслям, т. е. Х₀ =Y. Для выполнения собственного задания каждая отрасль нуждается в продукции других отраслей. Если бы все отрасли подсчитали потребности и подали заявки в некоторый центр, то оказалось бы, что суммарная потребность составляет X₁ =АХ₀=АY. Вектор X₁ можно рассматривать как промежуточную продукцию, необходимую для производства Х₀. Но под обеспечение производства X₁ тоже нужна промежуточная продукция: X₂ =АХ₁ =А²Y. Рассуждая так и далее, мы приходим к выводу, что

Х=Х₀+Х₁+Х₂+...+Х_k+... = Y+АY+А²Y+...+A^kY+... =

= (е+а+а²+…+а^k+...)Y.

Полные затраты можно разложить на прямую и косвенную составляющие. Прямые затраты осуществляются непосредственно при производстве данного продукта, а косвенные А²+А³+…+А^k+... относятся к предшествующим стадиям производства. Они осуществляются не прямо, а через посредство других ингредиентов, входящих в данный продукт. Элементы матрицы А² представляют собой косвенные затраты первого порядка, элементы матрицы А³ - косвенные затраты второго порядка и т. д.

Пример 1. Рассматривается трехотраслевой МОБ. Известна матрица коэффициентов прямых материальных затрат и задан вектор конечного продукта:

.

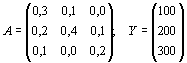Определить валовое производство X, обеспечивающее заданный конечный продукт.

Для ответа на поставленный вопрос необходимо составить и решить систему линейных уравнений (Е-А)Х = Y.

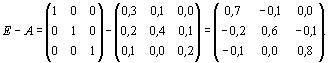
Получим соответствующую систему уравнений

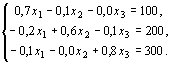
Решим систему методом Крамера. Если определитель системы отличен от нуля, то система имеет единственное решение, которое находится по формулам

где - определитель, который получается из заменой j-го столбца столбцом свободных членов.

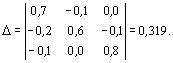
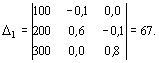
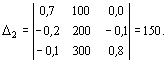
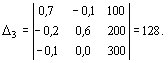
Применяя формулы Крамера, получаем решение системы:

Пример 2. Вычислить изменение межотраслевых потоков, если известна матрица коэффициентов полных материальных затрат и задан вектор изменения конечного продукта:

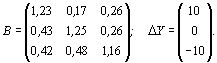
Изменение межотраслевых потоков вычисляется по формулам

Вектор изменения валового производства определяется следующим образом:

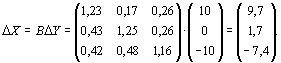
Кроме того, нам необходимо знать матрицу А. Из формулы В=(Е-А)^-1 следует, что

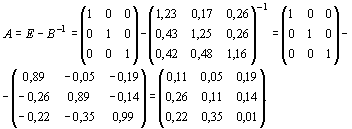
Теперь, отвечая на поставленный вопрос, получаем:

и т.д.