ТЕОРИЯ ИГР

Пример 1. Рассмотрим игру, представленную платежной матрицей

.

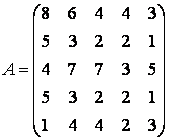Решение

; . Элементы стратегий А₂ и А₄ одинаковы, одну из них можно исключить. Все элементы стратегии А₂ меньше элементов стратегии А₁, следовательно, А₂ можно исключить. Все элементы А₅ меньше А₃, исключаем А₅.

.

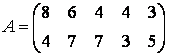Для второго игрока, сравнивая В₁ и В₄, исключаем В₁; сравнивая В₂ и В₅ , исключаем В₂.

В результате преобразований получим матрицу

.

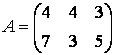Пример 2. Найти решение игры, заданной платежной матрицей

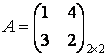
Решение

Игра не имеет седловой точки. Оптимальное решение следует искать в области смешанных стратегий. Построим на плоскости отрезки, соответствующие стратегиям второго игрока.

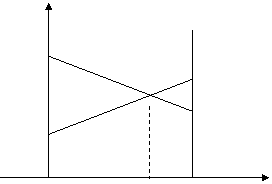
К

0 х₂ х₁ 1 х

По формулам

,

,

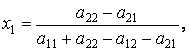
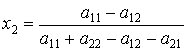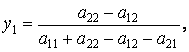
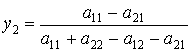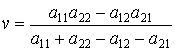
находим оптимальные стратегии и цену игры .

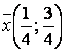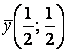Ответ. Оптимальные смешанные стратегии игроков и , цена игры составляет

Данный ответ означает следующее:

- если первый игрок с вероятностью будет применять первую стратегию и с вероятностью вторую, то при достаточно большом количестве игр с данной матрицей его выигрыш в среднем составит не менее ;

- если второй игрок с вероятностью будет применять первую стратегию и с вероятностью вторую, то при достаточно большом количестве игр с данной матрицей его проигрыш в среднем составит не более .

Пример 3. Найти решение игры, заданной платежной матрицей

.

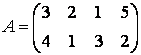Решение

Игра не имеет седловой точки. Оптимальное решение следует искать в области смешанных стратегий. Построим на плоскости отрезки, соответствующие стратегиям второго игрока.

В₄ В₁

В₁ В₃

В₂ К В₄

В₃ В₂

0 х₂ х₁ 1 х

Нижней границей выигрыша для игрока А является ломаная В₃ К В₂. Стратегии В₃ и В₂ являются активными стратегиями игрока В. Точка их пересечения К определяет оптимальные стратегии игроков и цену игры. Второму игроку не выгодно применять стратегии В₁ и В₄, поэтому вероятность их применения равна 0, т.е. у₁=0 и у₄=0.

Решение игры сводится к решению игры с матрицей

.

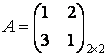По формулам находим оптимальные стратегии и цену игры:

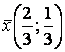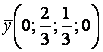Ответ. Оптимальные смешанные стратегии игроков и , цена игры составляет

Данный ответ означает следующее:

- если первый игрок с вероятностью будет применять первую стратегию и с вероятностью вторую, то при достаточно большом количестве игр с данной матрицей его выигрыш в среднем составит не менее ;

- если второй игрок с вероятностью будет применять вторую стратегию, с вероятностью третью и не применять первую и четвертую, то при достаточно большом количестве игр с данной матрицей его проигрыш в среднем составит не более .

Пример 4. Найти решение игры, заданной платежной матрицей

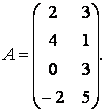
Решение

Игра не имеет седловой точки. Оптимальное решение следует искать в области смешанных стратегий. Построим на плоскости отрезки, соответствующие стратегиям второго игрока.

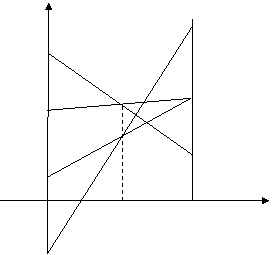
А₄

А₂

К М А₃

А₁ А₁

А₃ v А₂

А₄ 0 у₂ у₁ 1 y

Верхней границей проигрыша для игрока В является ломаная А₂КМА₄. Стратегии А₁ и А₂ являются активными стратегиями игрока А. Точка их пересечения К определяет оптимальные стратегии игроков и цену игры. Первому игроку не выгодно применять стратегии А₃ и А₄, поэтому вероятность их применения равна 0, т.е. х₃=х₄=0.

Решение игры сводится к решению игры с матрицей :

.

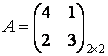Пример 5. Найти решение игры, заданной платежной матрицей

,

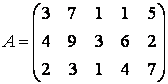Решение

Игра не имеет седловой точки. Оптимальное решение следует искать в области смешанных стратегий.

Для определения оптимальной стратегии игрока А имеем следующую задачу линейного программирования.

.

Для оптимальной стратегии В имеет следующую задачу линейного программирования:

.

Оптимальные решения пары двойственных задач имеют вид

.

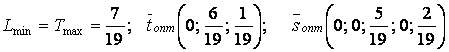Учитывая соотношения между х_i и t_i; y_j и s_j, а также равенство находим оптимальные стратегии игроков и цену игры

.

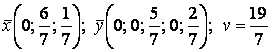Пример 6. В приближении посевного сезона фермер Иванов имеет четыре альтернативы: A₁ - выращивать кукурузу, A₂ - выращивать пшеницу, A₃ - выращивать овощи, A₄ - использовать землю под пастбища. Платежи, связанные с указанными возможностями, зависят от количества осадков, которые условно можно разделить на четыре категории: B₁ - сильные осадки, B₂ - умеренные осадки, B₃ - незначительные осадки,
B₄ - засушливый сезон.

Платежная матрица в тысячах рублей оценивается следующим образом:

Что должен посеять Иванов?

Решение

1. Согласно критерию Вальда рекомендуется применять максимальную стратегию.

Следует сеять пшеницу.

2. Воспользуемся критерием Сэвиджа. Составим матрицу рисков, элементы которой находим по формуле

.

Оптимальная стратегия определяется выражением

.

Найдем .

В соответствии с этим критерием следует сеять пшеницу.

3. Воспользуемся критерием Гурвица. Оптимальная стратегия определяется по формуле

,

где - степень оптимума и изменяется в диапазоне , предположим ,

,

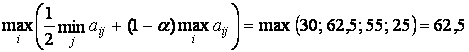т.е. следует принять решение о посеве пшеницы.

4. Если принять известным распределение вероятностей для различных состояний природы, например считать эти состояния равновероятными

,

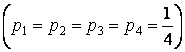то для принятия решения следует найти математические ожидания выигрыша

,

,

,

,

так как максимальное значение имеет М₂, то следует сеять пшеницу.