ПРОИЗВОДСТВЕННЫЕ ФУНКЦИИ
Пример
1. Пусть
некоторое производство можно описать с помощью функции
Кобба - Дугласа. В настоящее время один работник производит в
месяц продукции на 1 млн. руб. Общая численность
работников 1000 чел. Основные фонды
оцениваются в 10 млрд. руб. Известно, что
для увеличения выпуска продукции на 3% следует увеличить или стоимость фондов
на 6%, или численность работников на 9%.
1. Составить для данного предприятия
производственную функцию, определив коэффициенты эластичности.
2. Определить среднюю и предельную производительность труда.
3. Определить среднюю и предельную фондоотдачу.
4. Найти нормы замещения ресурсов, предельные нормы замещения
ресурсов.
5. Определить численность
работников, если стоимость основных фондов увеличить в 100 раз, уменьшить в 100
раз.
Решение. Производственная функция Кобба - Дугласа имеет вид
![]() ,
,
где х1
- затраченный труд; х2 - капитал.
Найдем коэффициенты
эластичности.
По условию х1= 1000 чел., х2=1010 руб.
Тогда у
= х1 · 1 000 000= 109 (руб) - объем
продукции в стоимостном выражении.
Перепишем функцию Кобба -
Дугласа в относительных приращениях:
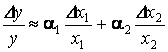 ,
,
где Dу/у - прирост объема продукции;
Dх1/х1 - прирост
трудовых ресурсов;
Dх2/х2 - прирост
фондов.
Нам известно, что для увеличения
выпуска продукции на 3% (Dу/у = 3%)
следует увеличить стоимость
фондов на 6% (Dх2/х2 = 6%), т.е. 0,03=α1·0
+ α2 ·0,06,
либо численность работников
увеличить на 9% (Dх1/х1 =9%), т.е.
0,03 = α1 ·0,09 + α
2 ·0.
Тогда
коэффициенты эластичности:
α 2= 1/2, α 1=1/3,
α 1 + α 2 = 1/3 +1/2
=5/6 .
Теперь производственная функция имеет вид:
![]() .
.
 .
.
Итак, производственная функция имеет вид: ![]() .
.
Определим среднюю и предельную производительность
труда:
![]() =
= ![]() =106 - средняя производительность труда;
=106 - средняя производительность труда;
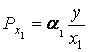 =
=![]()
![]() · 106 = 333333
· 106 = 333333![]() - предельная производительность труда.
- предельная производительность труда.
3. Определим среднюю и
предельную фондоотдачу:
![]() =109 / 1010 = 0,1 - средняя фондоотдача;
=109 / 1010 = 0,1 - средняя фондоотдача;
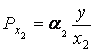 =
=![]() · 0,1 = 0,05 -
предельная фондоотдача.
· 0,1 = 0,05 -
предельная фондоотдача.
4. Найдем нормы замещения
ресурсов.
h1= х2/ х1 = 1010 / 103 = 107
- норма замещения первого ресурса вторым.
h2=х1/ х2=103/1010=10-7 - норма
замещения второго ресурса первым.
![]() 2/3 · 107=6666666
2/3 · 107=6666666![]() - предельная норма замещения первого ресурса вторым.
- предельная норма замещения первого ресурса вторым.
R21=1/R12= 3/2·10-7 = 0,00000015 - предельная норма замещения второго
ресурса первым.
Определим численность работников,
необходимую для сохранения объема выпуска продукции, если стоимость основных
средств увеличить в 100 раз; уменьшить в 100 раз.
а) Увеличение в
100 раз.
х2 увел =100 х2= 1012;
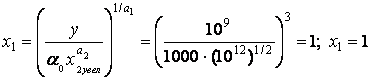 чел.
чел.
б) Уменьшение в 100 раз.
х2 умен = х2 /100=108.
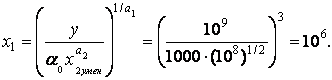
![]() чел.
чел.
Пример 2. Дана производственная
функция ![]() , где y -
объем товарной продукции в стоимостном
выражении, х1 - фонд заработной платы, х2 -
стоимость основных фондов. Произошло изменение используемых ресурсов:
фонд заработной платы уменьшился на 3%, стоимость основных фондов возросла на
2%. На сколько процентов при этом изменятся:
, где y -
объем товарной продукции в стоимостном
выражении, х1 - фонд заработной платы, х2 -
стоимость основных фондов. Произошло изменение используемых ресурсов:
фонд заработной платы уменьшился на 3%, стоимость основных фондов возросла на
2%. На сколько процентов при этом изменятся:
1) объем товарной продукции;
2) производительность труда;
3) фондоотдача.
Решение. Решим задачу двумя способами.
Первый способ. Производственная функция имеет вид: ![]() , и это есть 100%. По условию, х1
уменьшилось на 3%, т.е. стало 0,97х1, а х2 на 2% увеличилось,
т.е. стало 1,02х2. Тогда новое значение производственной
функции:
, и это есть 100%. По условию, х1
уменьшилось на 3%, т.е. стало 0,97х1, а х2 на 2% увеличилось,
т.е. стало 1,02х2. Тогда новое значение производственной
функции:
![]()
Узнаем, сколько процентов
составляет ун по
отношению к у:
у - 100%; ун
- Z %.
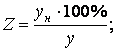
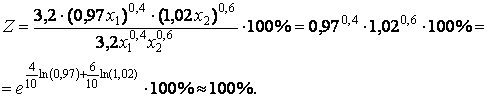
Таким образом, объем продукции практически не изменился.
Производительность труда
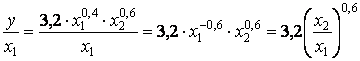 .
.
При изменении х1
и х2 новая производительность труда будет
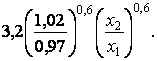
Пусть прежнее значение производительности труда ![]() составляет 100%. Тогда
новое значение
составляет 100%. Тогда
новое значение
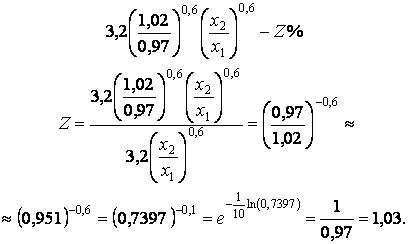
Так как Z = 103%, то произошло
увеличение производительности труда на 3%.
Фондоотдача
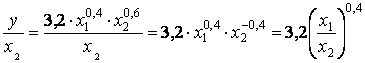 .
.
Так как х1 и х2
изменились, то новая фондоотдача составит:
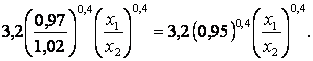
Составим пропорцию
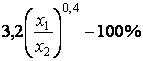 ;
; 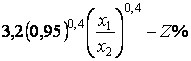 .
.
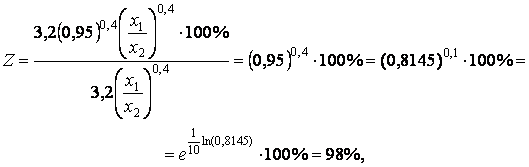
т.е. фондоотдача уменьшилась на 100% - 98% = 2%.
Второй способ. Прологарифмируем производственную функцию:
![]() .
.
Продифференцируем полученное равенство
 .
.
Тогда
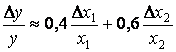 .
.
Величины ![]()
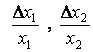 выражают относительные
приращения величин х1 и х2 и в нашем примере они соответственно равны
-0,03 и 0,02. Тогда изменение объема товарной продукции
выражают относительные
приращения величин х1 и х2 и в нашем примере они соответственно равны
-0,03 и 0,02. Тогда изменение объема товарной продукции
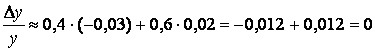 .
.
Следовательно, объем товарной продукции не
изменился.
Производительность труда
определяется равенством
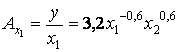 .
.
Логарифмируя это равенство, получим
![]() ;
;
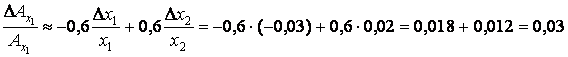 .
.
Таким образом, производительность труда возросла на
3%.
Фондоотдача
выражается формулой
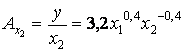 .
.
Логарифмируя это равенство, получим
![]() ,
,
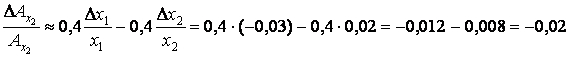 .
.
Следовательно, фондоотдача снизилась на 2%.