Окружность

Определение 1. Геометрическое место точек, расстояние от каждой из которых до данной точки О, называемой центром, есть величина постоянная, называется окружностью.

Выведем уравнение окружности. Обозначим постоянное расстояние из определения окружности R. Введем систему координат: центр системы совпадает с точкой О. Возьмем произвольную точку M (x, y) на окружности и составим уравнение, связывающее ее координаты x и y (рис. 1).

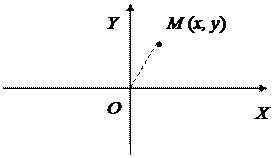
Рис. 1

По определению окружности MО = R, отсюда:

.

Освободимся в последнем равенстве от радикала возведением в квадрат обеих частей равенства. В результате получим:

— каноническое уравнение окружности.

Окружность является частным случаем эллипса, когда большая и малая полуоси равны, с = 0, фокусы сливаются в центр. Эксцентриситет окружности равен нулю.

.
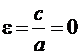