Коллинеарные и ортогональные векторы

Определение 1. Два n-мерных вектора и называются коллинеарными, если найдется число такое, что = · .

Рассмотрим два коллинеарных вектора и . Так как они коллинеарны, то = · , или (a_1, a_2, …, a_n)=(l b_1, l b_2, …, l b_n ). Следовательно, a₁=l b_1, a₂=l _2, …, a_n=l b_n.

Выражая из этих равенств l, получим

- условие коллинеарности.

Для того чтобы два вектора были коллинеарными, необходимо и достаточно, чтобы их координаты были пропорциональны.

Найдем угол между коллинеарными векторами.

.

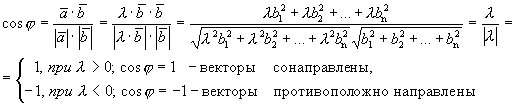Определение 2. Два ненулевых n-мерных вектора и называются ортогональными, или перпендикулярными, если угол между ними равен 90°.

,

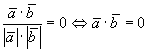- условие ортогональности.

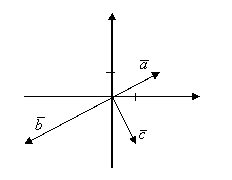
Пример. (2;1), (-4;-2), (1;-2).

Y = ,

· =2 · 1+1 · (-2)=0.

1 Векторы и коллинеарны,

1 Х векторы и ортогональны.