Действия над комплексными числами.
Определение 1. Суммой (разностью) двух комплексных чисел ![]() и
и ![]() называется
комплексное число
называется
комплексное число ![]() , определяемое равенством
, определяемое равенством
![]() .
.
Re z = Re z1+Re z2, Im z = Im z1+Im z2.
Если комплексные числа изобразить векторами, то их сумму и разность можно найти как сумму и разность этих векторов на плоскости.
Найдем различные степени мнимой единицы.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , …
, …
Следовательно,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Определение 2. Произведением комплексных
чисел ![]() и
и ![]() называется
комплексное число, которое получится, если перемножить эти числа как двучлены
по правилам алгебры.
называется
комплексное число, которое получится, если перемножить эти числа как двучлены
по правилам алгебры.
![]() ,
,
Re z = а1а2-b1b2, Im z = a1b2 + a2b1.
Если комплексные числа
записаны в тригонометрической форме
![]() ,
, ![]() ,
,
то
![]()
![]() ,
,
![]() .
.
![]() ,
, ![]() .
.
При перемножении комплексных чисел модуль произведения равен произведению модулей, а аргумент равен сумме аргументов.
Определение 3. Комплексные
числа ![]() и
и ![]() называются
сопряженными.
называются
сопряженными.
Сопряженные числа обладают свойствами:
![]() ,
,
![]() .
.
Произведение сопряженных
чисел равно квадрату модуля каждого из них.
Определение 4.
Чтобы разделить два комплексных числа z1 на z2, надо умножить делимое и
делитель на сопряженное делителю комплексное число. Тогда в знаменателе дроби
получится действительное число.
![]() .
.
Формула для деления
комплексных чисел, заданных в тригонометрической форме:
![]() .
.
Покажем, что эта формула
верна. Умножим результат на z2.
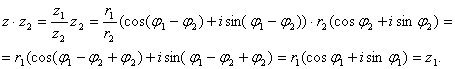
Следовательно, частное
найдено верно.
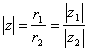 ,
, ![]() .
.
При делении комплексных чисел модуль частного равен частному модулей, а аргумент частного равен разности аргументов.
Замечание 1. Если правила действия над комплексными числами применить к действительным числам, рассматривая их как частный случай комплексных, то они совпадут с арифметическими правилами действия над числами.
Замечание 2. Если в определениях 1,2,4, заменить сопряженным числом каждое комплексное число, то и результат будет сопряженным соответственно к исходным результатам.
Теорема 1. Если в многочлен ![]() , где Ai ÎR,
, где Ai ÎR, ![]() подставить вместо
подставить вместо ![]() число
число ![]() , а затем сопряженное число
, а затем сопряженное число
![]() , то результаты этих подстановок будут взаимно сопряженными.
, то результаты этих подстановок будут взаимно сопряженными.