Тригонометрическая форма записи комплексного числа.
 Каждому комплексному числу из множества C можно поставить в соответствие
точку координатной плоскости. Точке
Каждому комплексному числу из множества C можно поставить в соответствие
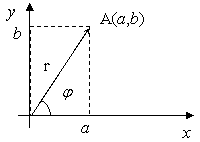
точку координатной плоскости. Точке ![]() соответствует
соответствует
точка ![]() . Вектор
. Вектор ![]() считают геометрическим изображением
комплексного числа, а всю плоскость XOY –комплексной плоскостью.
считают геометрическим изображением
комплексного числа, а всю плоскость XOY –комплексной плоскостью.
Обозначим длину вектора ![]() .Угол, который вектор
.Угол, который вектор ![]() образует с
положительным
образует с
положительным
направлением ![]() обозначим
обозначим ![]() . Из DАСО:
. Из DАСО:
Re z = ![]() , Im z =
, Im z = ![]() ,
,
-
![]()
-
тригонометрическая форма записи комплексного числа.
Величина ![]() называется модулем
комплексного числа.
называется модулем
комплексного числа.
Угол ![]() называется аргументом
комплексного числа.
называется аргументом
комплексного числа.
Аргумент комплексного числа может
быть положительным, отрицательным и нулевым. Аргумент определяется не
однозначно, а с точностью до слагаемого ![]()
Действительное число ![]() R
может быть записано в тригонометрической форме.
R
может быть записано в тригонометрической форме.
При ![]() >0
>0 ![]() .
.
При ![]() <0
<0 ![]() .
.
½0½=0, Arg 0 – любой угол,
![]() .
.