Общее решение однородной системы

Система

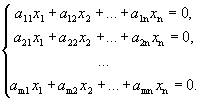(1)

всегда имеет тривиальное решение. Если ранг матрицы, составленной из коэффициентов при неизвестных, меньше числа неизвестных, то система (1) имеет нетривиальные решения.

1) r(A)=n - система (1) имеет только тривиальное решение:

2) r(A)=r<n - система (1) имеет нетривиальные решения.

Количество свободных переменных во втором случае будет равно n-r, а базисных r. Давая свободным переменным произвольные значения, мы будем получать различные решения системы (1), т.е. любому вектору размерности n-r

(с_r+1, c_r+2, …, c_n)

будет соответствовать решение системы (1)

(с₁, c₂, …, c_r, c_r+1, …, c_n).

Определение. Фундаментальной системой решений однородной системы (1) называется максимальная линейно независимая система решений системы (1). Фундаментальная система содержит n-r линейно независимых решений системы (1).

Чтобы получить фундаментальную систему решений, нужно в (n-r)-мерном пространстве взять линейно независимую систему из n-r векторов и по ним построить соответствующие решения системы (1). Полученные решения будут образовывать фундаментальную систему решений . Так как эта система максимальна, то любое решение системы (1) можно представить в виде линейной комбинации решений фундаментальной системы . Полученное выражение является общим решением однородной системы (1).

Пример. 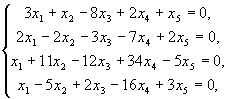r(A)=2,

x₁, x₂ - базисные, x₃, x₄, x₅ - свободные. Отбросим два последних уравнения:

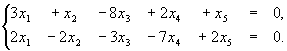
Выразим базисные переменные.

Умножим первое уравнение на 2 и сложим со вторым. Результат разделим на 8.

Умножим первое уравнение на 2, второе на -3 и сложим полученные уравнения. Результат разделим на 8.

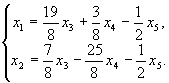
В качестве значений свободных переменных возьмем координаты векторов трехмерного базиса.

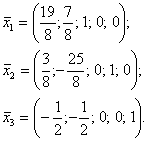- фундаментальная система решений,

- общее решение однородной системы.

Сумма общего решения однородной системы (1) с любым решением соответствующей неоднородной системы является общим решением неоднородной системы.