Метод Гаусса

Определение 1. Элементарными преобразованиями системы называются:

1) умножение уравнения на число, отличное от нуля;

2) прибавление к одному уравнению другого уравнения, умноженного на некоторое число, отличное от нуля.

3) перестановка двух уравнений;

4) отбрасывание уравнения 0=0.

Если получено уравнение 0=k, то система несовместна.

Метод Гаусса состоит в приведении системы к диагональному виду путем последовательного исключения неизвестных. Количество исключенных неизвестных равно числу линейно независимых уравнений. Переменная считается исключенной, если она содержится только в одном уравнении с коэффициентом 1.

Пример.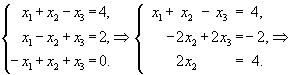

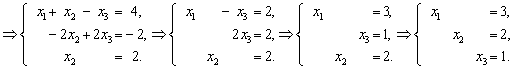Получено решение системы .

Метод Гаусса удобно применять к расширенной матрице системы, левую часть которой с помощью элементарных преобразований матрицы нужно привести к единичной матрице.

Пример. Рассмотрим систему из предыдущего примера. Составим расширенную матрицу:

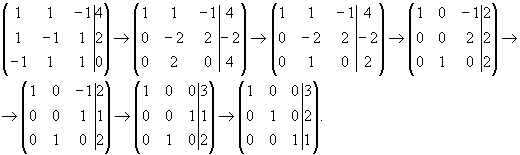
Получено решение системы .