Решение произвольных систем

линейных неоднородных уравнений

Пусть дана неоднородная система m линейных уравнений с n неизвестными

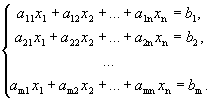
Предположим, что система совместна, т.е. r(A)==r. Следовательно, существует минор порядка r матрицы А, отличный от нуля. Предположим, что он расположен в левом верхнем углу матрицы. Если это не так, то можно переставить уравнения и перенумеровать неизвестные.

.

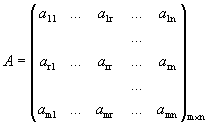Первые r уравнений системы линейно независимы. Остальные выражаются через них. Следовательно, их можно отбросить.

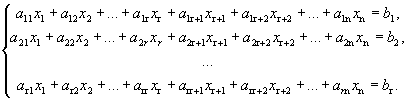
Определение 1. Переменные, коэффициенты при которых образуют минор, отличный от нуля (базисный минор), называются базисными переменными (x₁, x₂, …, x_r). Остальные переменные x_r+1, …, x_n называются свободными.

Дадим свободным переменным произвольные числовые значения x_r+1=с_r+1, x_r+2=с_r+2, …, x_n=c_n.

Запишем систему в виде

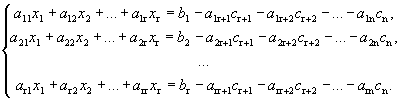
Мы получили систему из r линейных уравнений с r неизвестными, определитель которой отличен от нуля. Она имеет единственное решение.

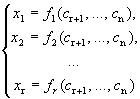- общее решение.

Определение 2. Выражение базисных переменных через свободные называется общим решением системы.

Определение 3. Решение системы, полученное из общего при конкретных значениях свободных переменных, называется частным решением. Частных решений у системы бесконечно много, все они содержатся в общем решении.

Определение 4. Частное решение, полученное из общего, когда свободные переменные равны нулю, называется базисным решением системы.

Определение 5. Базисное решение, координаты которого неотрицательны, называется опорным решением системы.

Пример.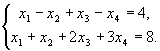

, r(A)==2.

Переменные х₁ и х₂ - базисные, х₃ и х₄ - свободные.

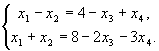
Сложим уравнения и результат разделим на 2. Вычтем из второго уравнения первое и результат разделим на 2. Получим

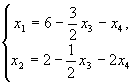- общее решение решение.

Из него можно получить частные и базисное решения.

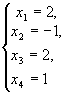- частное решение, полученное при х₃=2 и х₄=1.

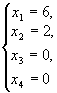- базисное решение при х₃=х₄=0. Оно же является опорным.