Решение системы с помощью

обратной матрицы

Пусть дана неоднородная система n линейных уравнений с n неизвестными

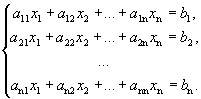
Ее можно представить в матричном виде .

Пусть определитель матрицы, составленной из коэффициентов при неизвестных, не равен нулю. Следовательно, система имеет единственное решение. Если , то матрица А имеет обратную матрицу А^-1. Умножим обе части равенства слева на А^-1.

.

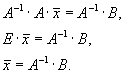Чтобы найти решение системы, надо найти обратную матрицу к матрице, составленной из коэффициентов при неизвестных, и умножить ее справа на матрицу-столбец свободных членов В.