Решение системы с помощью

формул Крамера

Рассмотрим неоднородную систему n линейных уравнений с n неизвестными:

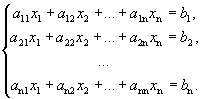
Теорема (теорема Крамера). Если определитель матрицы, составленной из коэффициентов при неизвестных, отличен от нуля (), то система имеет единственное решение, которое можно найти по формулам Крамера:

, где - главный определитель, - j-й вспомогательный определитель, который получен из определителя заменой j-го столбца столбцом свободных членов.

Пример.

,

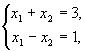
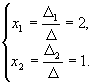
Если главный определитель равен нулю и хотя бы один их вспомогательных определителей отличен от нуля, то система решений не имеет.

Если главный определитель и все вспомогательные определители равны нулю, то система имеет бесконечно много решений.