Условие совместности
Рассмотрим неоднородную систему:
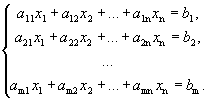
Рассмотрим матрицы:
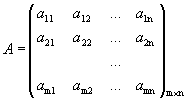 и
и 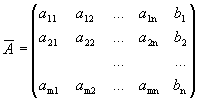 .
.
Матрица
![]() называется расширенной
матрицей системы.
называется расширенной
матрицей системы.
Теорема (теорема Кронекера - Капелли). Неоднородная система линейных уравнений совместна тогда и только тогда, когда ранг матрицы, составленной из коэффициентов при неизвестных, равен рангу расширенной матрицы.
Доказательство. Необходимость. Пусть система совместна, тогда найдутся числа с1, с2, …, сn, при подстановке которых в систему мы получим m тождеств, которые можно записать в виде одного векторного тождества:
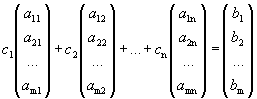 .
.
Следовательно,
вектор-столбец свободных членов является линейной
комбинацией векторов-столбцов матрицы А, тогда добавление его к
системе векторов-столбцов матрицы А не меняет ранга системы. Отсюда r(A)=![]() .
.
Достаточность. Пусть r(A)=![]() =r. Следовательно, существует линейно независимая подсистема из r векторов-столбцов
матрицы A. Она
же будет содержатся и в матрице
=r. Следовательно, существует линейно независимая подсистема из r векторов-столбцов
матрицы A. Она
же будет содержатся и в матрице ![]() . Так как эта система максимальна, то вектор-столбец
свободных членов будет выражаться через эти r векторов-столбцов. Следовательно,
вектор-столбец свободных членов можно представить в виде линейной комбинации
всех векторов-столбцов матрицы А, т.е. найдутся числа с1, с2, …, сn
такие, что вектор-столбец будет представлен в виде
. Так как эта система максимальна, то вектор-столбец
свободных членов будет выражаться через эти r векторов-столбцов. Следовательно,
вектор-столбец свободных членов можно представить в виде линейной комбинации
всех векторов-столбцов матрицы А, т.е. найдутся числа с1, с2, …, сn
такие, что вектор-столбец будет представлен в виде
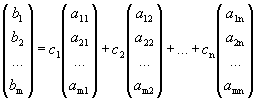 .
.
Следовательно, числа с1, с2, …, сn являются решением системы, т.е. она совместна.