Метод интегрирования по частям

в неопределенном интеграле

Теорема. Пусть функции u и υ определены и дифференцируемы на некотором промежутке Т и функция du·υ имеет на этом промежутке первообразную. Тогда функция u·dυ также имеет первообразную на промежутке Т, причем справедлива формула

òudυ = uυ - òυdu.

Доказательство. Найдем дифференциал от их произведения u · υ.

d(uυ) = du·υ + u·dυ.

Проинтегрируем обе части этого равенства.

òd(uυ) = ò(du·υ + u·d υ).

uυ = ò υdu + ò udυ,

ò udυ = uυ - ò υdu - формула интегрирования по частям.

С помощью этой формулы первообразная частично находится, и оставшиеся интегральные слагаемые, как правило, - проще исходного интеграла.

Данная формула применяется к интегралам следующих видов.

1) ,

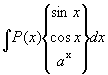где P(x) - многочлен, его выбирают в качестве u.

2) .

В качестве u выбирают трансцендентную функцию.

3) Циклические интегралы – это те, в которых подынтегральная функция представляется в виде произведения двух функций, мало меняющихся при интегрировании и дифференцировании.

Пример 1.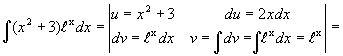

.

Пример 2.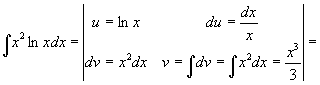

=.