Метод замены переменной

в неопределенном интеграле

Теорема 1. Пусть функция х= φ(t) определена и дифференцируема на некотором промежутке Т, а Х – множество значений этой функции, на котором определена функция f(x). Тогда, если функция f(x) имеет первообразную на множестве Х, то на множестве Т справедлива формула

ò f(x)dx = ò f(φ(t))φ'(t)dt.

Доказательство. Найдем дифференциалы обеих частей равенства:

d(ò f(x)dx) = f(x)dx = f(φ(t))d(φ(t)) = f(φ(t))φ'(t)dt,

d(ò f(φ(t))φ'(t)dt) = f(φ(t))φ'(t)dt.

Дифференциалы обеих частей равны, значит, сами интегралы могут отличаться лишь на постоянное слагаемое.

При подходящем выборе функции φ(t) интеграл становится значительно проще исходного интеграла.

Пример.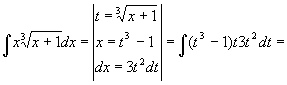

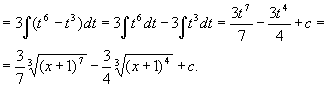
Новую переменную можно не выписывать явно. В таких случаях говорят о введении постоянных и переменных под знак дифференциала или о тождественном преобразовании дифференциала.

Пример 1. ,

.

Пример 2. ,

d (sin x) = cos х dx.