Несобственные интегралы первого рода

Пусть функция y = f(x) определена и непрерывна на [a, ¥) (рис. 1).

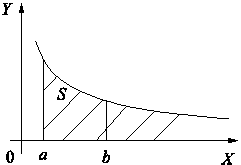
Рис. 1

Рассмотрим интеграл 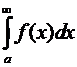. Вычисление несобственного интеграла можно свести к вычислению обычного определенного интеграла и нахождению предела ().

.

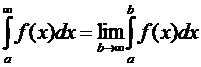Если предел, стоящий справа, существует и конечен, то несобственный интеграл называется сходящимся и он равен значению этого предела. В противном случае интеграл называется расходящимся.

Пусть F(x) — одна из первообразных f(x), тогда

.

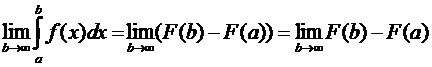Обозначим .

Тогда 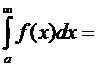F(¥) – F(a) — обобщенная формула Ньютона-Лейбница (для вычисления несобственного интеграла).

Пример 1. Вычислить несобственный интеграл от функции 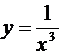по промежутку [1, ∞) (рис. 2).

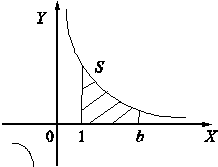
Рис. 2

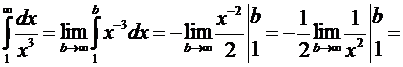
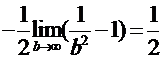
Интеграл сходится и равен .

Пример 2. Вычислить несобственный интеграл от функции 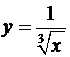по промежутку [1, ∞).

= .

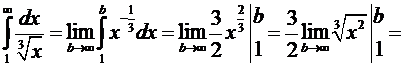
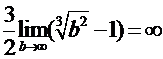Интеграл расходится.

Аналогично определяются несобственные интегралы первого рода по другим неограниченным промежуткам.

Рассмотрим интеграл по промежутку (–¥; b].

.

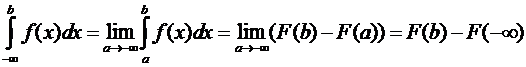Рассмотрим интеграл по промежутку (–¥: + ¥).

.

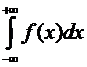Данный интеграл сводится к предыдущим двум типам. Возьмем произвольную точку с.

.

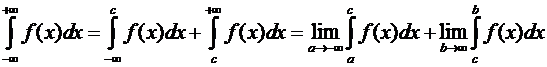Если оба предела, стоящие в правой части, существуют и конечны, то несобственный интеграл называют сходящимся, а иначе — расходящимся.

Пример 3. Вычислить несобственный интеграл от функции по промежутку (-∞, ∞) (рис. 3) .

Рис. 3

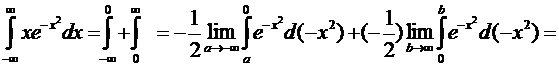
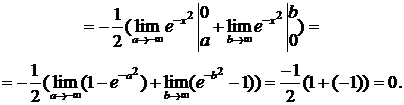
Данный интеграл сходится и равен нулю.