Вычисление определенного интеграла

Пусть функция y = f(x) непрерывна на [a,b], тогда функция будет являться первообразной. Пусть F(x) - любая первообразная функции f(x). Тогда по свойству первообразных Ф(х) = F(x) + С. Найдем С.

.

Следовательно, Ф(х) = F(x) - F(a).

Найдем Ф(b):

,

Ф(b) = F(b) - F(a).

Из двух последних равенств следует, что

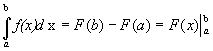– формула Ньютона – Лейбница.

С помощью этой формулы вычисляется определенный интеграл, если известна любая первообразная подынтегральной функции.