Геометрический смысл

определенного интеграла

Пусть функция у = f(x) определена и непрерывна на [a,b]. Разобьем отрезок [a,b] на n частей точками,

a = x₀ < x₁ < x₂ < ….< x_n = b.

Обозначим длину i-го отрезка разбиения . В каждом отрезке разбиения возьмем по точке с_i и составим интегральную сумму

. (*)

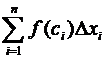Выясним, что представляет собой геометрически интегральная сумма. Каждое слагаемое равно площади прямоугольника со сторонами и (рис. 1).

Рис. 1

Из рисунка видно, что интегральная сумма равна площади ступенчатой фигуры, ограниченной ломаной, вписано-описанной около графика функции. При измельчении длин отрезков разбиения площадь этой фигуры будет неограниченно приближаться к площади фигуры, заключенной между графиком функции и осью ОХ на отрезке [а,b].

С другой стороны, предел интегральной суммы вида (*) при измельчении длин отрезков разбиения равен определенному интегралу 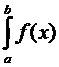dx, следовательно, определенный интеграл равен площади криволинейной трапеции, заключенной между графиком функции и осью ОХ на отрезке [a,b].