Определенный интеграл

Пусть функция у = f(x) определена, непрерывна (следовательно, ограничена) на [a,b]. Разобьем отрезок [a,b] на n произвольных частей точками

a = x₀< x₁ < x₂ < … < x_n = b.

Длину i -го отрезка разбиения обозначим

Dх_i = x_i - x_i-1, i = .

Внутри i -го отрезка разбиения выберем по произвольной точке с_i

с₁ с₂ с₃ с_n

Х

х₀ х₁ х₂ х₃ х_n-1 х_n

a b

и составим сумму

. (1)

Определение 1. Сумма вида (1) называется интегральной суммой функции f(x) по отрезку [a,b].

Определение 2. Если существует конечный предел интегральных сумм вида (1) при уменьшении длин отрезков разбиения, то он не зависит от способов разбиения отрезка. Этот предел называется определенным интегралом от функции f(x) по отрезку [a,b] и обозначается .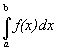

.
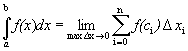