Свойства
производных
Теорема 1. Производная
постоянной функции равна нулю.
Доказательство. f(x) = c, "x0 Dy = f(x0 + Dx)
– f(x0)
= c – c = 0,
.
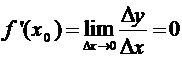Теорема 2. Если функции u, v, w дифференцируемы
в некоторой точке, то и их алгебраическая сумма также дифференцируема в этой
точке, причем производная алгебраической суммы равна алгебраической сумме
производных и выполняется равенство
.
Теорема 3. Если функции u и v
дифференцируемы в некоторой точке, то и их произведение также дифференцируемо в
этой точке, причем выполняется равенство
.
Следствие. Постоянный множитель можно выносить за знак производной.
.
Теорема 4. Если функции u и v
дифференцируемы в некоторой точке и функция v в этой точке отлична от нуля, то существует
производная частного в этой точке, причем
.
Теорема 5. (производная
сложной функции). Если функции y = f(z) и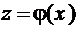 
— дифференцируемые функции своих
аргументов, то и их композиция является
дифференцируемой функцией, причем производная сложной
функции равна производной внешней функции по промежуточному аргументу,
умноженной на производную промежуточного аргумента по независимой переменной.
.
Теорема 6. (теорема Лагранжа). Конечное приращение дифференцируемой
функции равно произведению соответствующего приращения аргумента на производную
функции в некоторой промежуточной точке.
.
Доказательство. Проведем секущую к графику функции через точки 
и 
. Так как функция дифференцируема, то она имеет
касательную в каждой точке. Будем перемещать секущую параллельно, пока она не
станет касательной к графику в некоторой промежуточной точке с, 
(рис. 1).
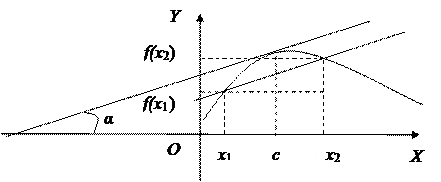
Рис. 1
Угловые коэффициенты
касательной и секущей равны kкас = kсек.
.
Отсюда
.
Теорема 7. (теорема Ролля). Между двумя нулями дифференцируемой функции всегда найдется хотя бы один
ноль производной.
Доказательство. Пусть f(x1)
= f(x2)
= 0. Из теоремы Лагранжа следует, что найдется точка с, 
, такая, что
.
Две последние теоремы носят
название теорем о конечных приращениях.