Логарифмическое дифференцирование

Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Дана функция y = f( x ). Возьмем натуральные логарифмы от обеих частей: ln y=ln f( x ). Продифференцируем обе части этого равенства:

.

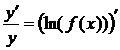Отсюда

.

Такая производная от логарифма функции называется логарифмической производной. Данный метод позволяет также вычислять производные показательно-степенных функций, степенных, рациональных и некоторых иррациональных функций.

Пример 1. Найти производную функции .

Прологарифмируем левую и правую части равенства:

.

Продифференцируем обе части последнего равенства:

.

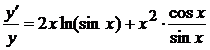Выразим из этого равенства искомую производную:

,

.

Пример 2. Найти производную функции .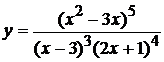

Прологарифмируем левую и правую части равенства:

.

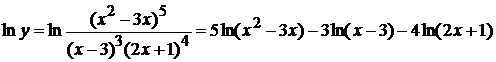Продифференцируем обе части последнего равенства:

.

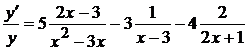Выразим из этого равенства искомую производную:

,

.
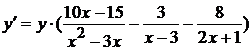
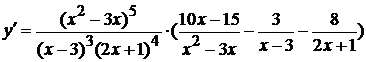