Выпуклость графика функции.

Точки перегиба графика

Определение 1. Функция y = f(x) называется выпуклой вверх (вниз) на интервале (a, b), если для и , выполняется условие:

- вверх,

- вниз.

Выясним геометрический смысл этих неравенств. Рассмотрим точки и , лежащие на графике.

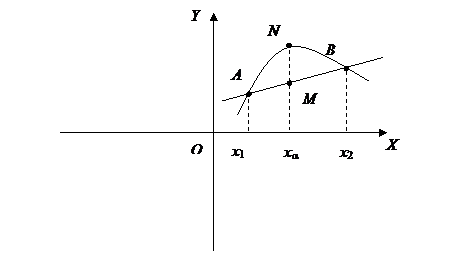
Рис. 1

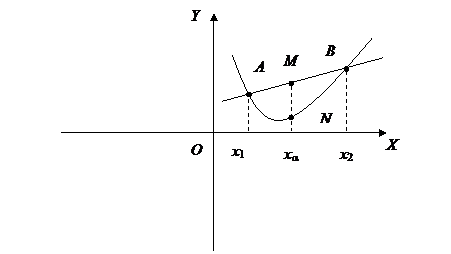
Рис. 2

Отрезок АВ состоит из точек М с координатами

, , где .

Первое неравенство означает, что (Рис. 1), а второе - (Рис. 2). Это говорит о том, что в первом случае (выпуклость вверх) точка N графика функции расположена выше соответствующей точки М отрезка АВ, а во втором случае (выпуклость вниз) - ниже.

Понятие выпуклости функции можно ввести с использованием касательных к графику.

Определение 2. График функции y = f(x) называется выпуклым или выпуклым вверх (вогнутым или выпуклым вниз) на интервале (a, b), если касательная к графику, проведенная в любой точке этого интервала, расположена над графиком функции (рис. а — выпуклый график) или под графиком функции (рис. б — вогнутый график).

Теорема 1. Если вторая производная дважды дифференцируемой функции на некотором интервале отрицательна (положительна), то график функции на данном интервале выпуклый (вогнутый).

Верна и обратная теорема.

Определение 3. Точки, в которой график функции меняет направление выпуклости, называют точками перегиба графика функции.

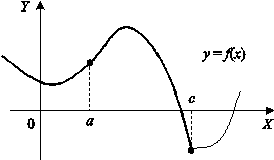
Рис. 3

Точка a (рис. 3) является точкой перегиба, а точка c нет, так как в этой точке функция не дифференцируема.

Теорема 2. (необходимый признак точки перегиба). Если точка х0 является точкой перегиба графика дважды дифференцируемой функции, то в этой точке вторая производная равна нулю: .

Определение 4.9. Точки, в которых вторая производная равна нулю или не существует, называются критическими точками второй производной. Если функция имеет точки перегиба, то они могут быть только в критических точках.

Теорема 3. (достаточный признак точки перегиба). Если вторая производная дважды дифференцируемой функции в некоторой точке равна нулю и при переходе через нее вторая производная меняет знак, то данная точка является точкой перегиба.