Основные теоремы о пределах

Теорема 1. (о предельном переходе в равенстве). Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.

Þ .

Теорема 2. (о предельном переходе в неравенстве). Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x), то предел функции f(x) в этой точке не превосходит предела функции g(x).

Þ .

Теорема 3. Предел постоянной равен самой постоянной.

.

Доказательство. f(x) = с, докажем, что .

Возьмем произвольное e > 0. В качестве d можно взять любое положительное число. Тогда при

.

Теорема 4. Функция не может иметь двух различных пределов в одной точке.

Доказательство. Предположим противное. Пусть

и .

По теореме о связи предела и бесконечно малой функции:

f(x) – A = — б.м. при ,

f(x) – B = — б.м. при .

Вычитая эти равенства, получим: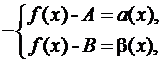

B – A = – .

Переходя к пределам в обеих частях равенства при , имеем: B – A = 0, т.е. B = A. Получаем противоречие, доказывающее теорему.

Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при , то и алгебраическая сумма имеет предел при , причем предел алгебраической суммы равен алгебраической сумме пределов.

.

Доказательство.

Пусть , , .

Тогда, по теореме о связи предела и б.м. функции:

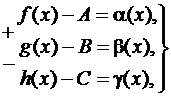где — б.м. при .

Сложим алгебраически эти равенства:

f(x)+g(x) – h(x) – (А+В – С) =,

где б.м. при функции.

По теореме о связи предела и б.м. функции:

А+В – С =

= .

Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при , то и произведение имеет предел при , причем предел произведения равен произведению пределов.

.

Следствие. Постоянный множитель можно выносить за знак предела.

.

Теорема 7. Если функции f(x) и g(x) имеют предел при , причем , то и их частное имеет предел при , причем предел частного равен частному пределов.

, .
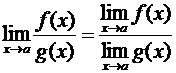