Бесконечные пределы. Односторонние пределы

Определение 1. Функция y=f(x) имеет предел при, равный +¥ (-¥), если "М>0 $ такое, что при всех х, удовлетворяющих , выполняется неравенство f(x)>М (f(x)<-М).

Определение 2. Число А называется пределом функции y=f(x) при слева, или левосторонним пределом, если "e>0 $ такое, что при всех х, удовлетворяющих условно , выполняется неравенство |f(x)-А|<e.

Определение 3. Число А называется пределом функции y=f(x) при справа, или правосторонним пределом, если "e>0 $ такое, что при всех х, удовлетворяющих неравенству , выполняется неравенство |f(x)-А|<e.

или - слева,

или 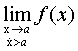- справа.

Функция имеет предел в некоторой точке, равный некоторому значению, тогда и только тогда, когда существуют и равны этому же значению оба односторонних предела.

==А ó =А.

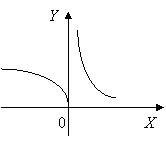
Пример.

Найти предел функции при .

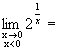0, +¥,

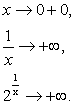
Предела функции при не существует.