Числовые последовательности.
Предел числовой последовательности
Определение 1. Функция, заданная на множестве натуральных чисел со значениями во множестве действительных чисел, называется числовой последовательностью.
Определение 1'. Числовой
последовательностью 
называется
занумерованное множество действительных чисел.
a1, a2, a3,
..., an...
Определение 2. Число А называется пределом
числовой последовательности 
, если для любого положительного e ("e>0)
существует номер n такой, что при всех номерах n>n
выполняется неравенство 
. Последовательность 
называется сходящейся
к числу А.
Кратко это можно записать так:
.
Пример. Рассмотрим последовательность 1, 
, 
, 
, ..., 
... .
Изобразим ее поведение
графически.
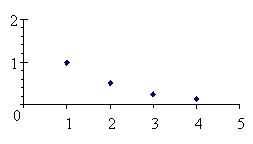
Из диаграммы видно, что с
ростом n члены последовательности стремятся к нулю. Покажем,
что предел этой последовательности равен нулю с помощью определения предела.
Возьмем в качестве e число 
. Найдем номер N такой, что при всех номерах n>n
выполняется неравенство 
,
e=
,
,
,
.
В качестве n можно взять следующее за числом 
натуральное число.
Аналогично можно подобрать номер N для произвольного e>0.
Определение 3. Числовая последовательность
имеет предел, равный +¥ (-¥), если для любого числа G>0
найдется номер n такой, что при всех номерах n>n
выполняется неравенство 
an>G
(an<-G).
Пример. Рассмотрим
последовательность
1, 3, 9, 27...
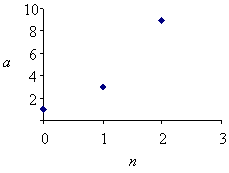
Возьмем G=1000,
3n>1000,
n>log31000.