Непрерывные проценты

Формула сложных процентов имеет вид

,

где Q – сумма вкладов по истечении n периодов, Q₀ – первоначальный вклад, p – процент начисления за период. (Аналогичные формулы используют в демографических расчетах прироста населения и в экономических прогнозах увеличения валового национального продукта.)

Пусть первоначальный депозит Q₀ помещен в банк под p=100% годовых, через год сумма составит

.

Предположим, что через полгода счет закрыт с результатом

,

и эта сумма вновь помещена в качестве депозита в том же банке. В конце года депозит будет составлять

.

Будем уменьшать срок размещения депозита в банке при условии его последующего размещения после изъятия.

При ежеквартальном повторении этих операций депозит в конце года составит

.

При ежемесячном повторении этих операций депозит в конце года составит

.

При ежедневном повторении этих операций депозит в конце года составит

.

При ежечасном повторении этих операций депозит в конце года составит

и т. д. Последовательность значений увеличения первоначального вклада

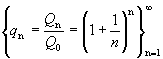
имеет предел при n®¥ , равный е.

Доход, который можно получить при непрерывном использовании процентов на проценты, может составить в год не более чем

.

Если р – процент начисления и год разбит на n частей, то через t лет сумма депозита достигнет величины

,

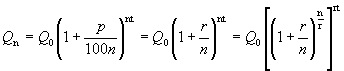где .

Если ввести новую переменную , то при n®¥ Þ m®¥.

.

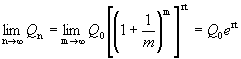Расчеты, выполненные по этой формуле, называют вычислениями по непрерывным процентам.

Пример. Темп инфляции составляет 1% в день. Насколько уменьшится первоначальная сумма Q₀ через полгода?

.

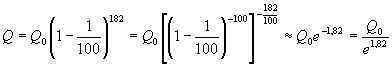Инфляция уменьшит начальную сумму примерно в шесть раз.