Замечательные
пределы
Теорема 1. Предел отношения синуса малой дуги к
самой дуге, выраженной в радианах, при стремлении величины дуги к нулю равен
единице.
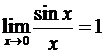 .
.
Доказательство. Рассмотрим случай ![]() . Так
как
. Так
как ![]() , то
, то 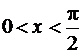 .
Построим тригонометрический круг и отложим в нем угол x радиан (рис.
1).
.
Построим тригонометрический круг и отложим в нем угол x радиан (рис.
1).
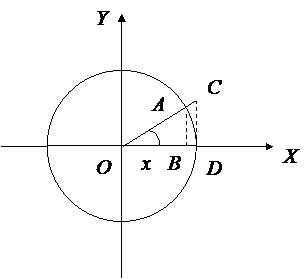
Рис. 1
Для площадей полученных фигур
справедливо неравенство
![]() .
.
Из данного неравенства с учетом
соотношений АВ = sin
x, CD
=tg x, OD = 1, получим
(площадь сектора с величиной дуги x радиан и радиуса r равна 1/2 x r2).
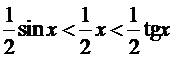 .
.
Разделим обе части неравенства на 1/2 sin
x > 0.
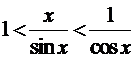 .
.
Запишем неравенство для обратных величин:
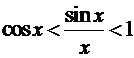 .
.
При ![]() левая и правая часть последнего неравенства
стремятся к единице, следовательно, по первому
признаку существования предела средняя часть неравенства также стремится к
единице, т.е.
левая и правая часть последнего неравенства
стремятся к единице, следовательно, по первому
признаку существования предела средняя часть неравенства также стремится к
единице, т.е.
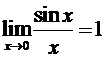 .
.
Случай ![]() сводится к предыдущему с использованием
четности функции y = sin x:
сводится к предыдущему с использованием
четности функции y = sin x:
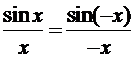 , где (-
x) > 0.
, где (-
x) > 0.
Теорема 2. Предел последовательности 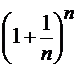 при
при ![]() равен
равен ![]() .
.
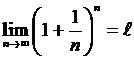 ,
, 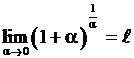 .
.