Приведение
квадратичной формы
к
каноническому виду
Рассмотрим квадратичную форму
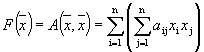 .
.
Выпишем ее матрицу и вектор-столбец переменных.
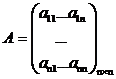 ;
; 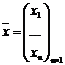 .
.
Тогда квадратичную форму можно представить в виде
![]() - матричная
запись квадратичной формы.
- матричная
запись квадратичной формы.
Пример 1. ![]() R.
R.
![]() .
.
![]() ,
, 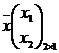 .
.
![]()
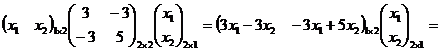
=![]() .
.
Определение 1. Если в некотором базисе квадратичная форма не содержит смешанных произведений переменных, т.е.
![]() ,
,
то этот базис называют
каноническим базисом данной квадратичной формы, а вид ![]() называют каноническим
видом данной квадратичной формы.
называют каноническим
видом данной квадратичной формы.
Определение 2. Нормированием вектора называется нахождение вектора того же направления единичной длины.
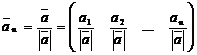 .
.
Теорема 1. Любую симметричную матрицу можно представить в виде A=UTDU, где D - диагональная матрица, у которой на диагонали расположены собственные числа матрицы А; U - матрица, составленная из нормированных собственных векторов матрицы А. Каждый вектор является столбцом.
Следовательно, любую квадратичную форму можно привести к каноническому виду с помощью некоторого ортогонального преобразования координат. Для всякой квадратичной формы существует канонический базис.
![]() .
.
Если ввести новые переменные по
формуле ![]() , то квадратичная форма примет следующий вид:
, то квадратичная форма примет следующий вид:
![]() - канонический
вид квадратичной формы.
- канонический
вид квадратичной формы.
Из данного равенства видно, что коэффициентами в каноническом виде являются собственные числа матрицы А.
Теорема 2 (закон инерции квадратичных форм). В любом каноническом виде квадратичной формы количество положительных и отрицательных коэффициентов постоянно.
Пример 2. Приведем квадратичную форму
![]() к каноническому
виду. Выпишем ее матрицу.
к каноническому
виду. Выпишем ее матрицу.
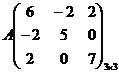 .
.
Найдем собственные значения матрицы квадратичной формы. Решим характеристическое уравнение.
![]() ,
,
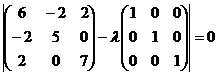 ,
,
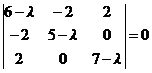 ,
,
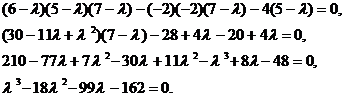
Корни данного уравнения являются делителями свободного члена. Разложим его на простые множители и подберем один из корней.
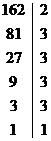
![]() -
является корнем. Разделим многочлен на линейный множитель l-3.
-
является корнем. Разделим многочлен на линейный множитель l-3.
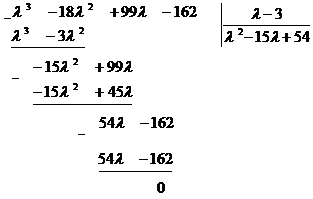
Найдем корни остатка.
![]()
Получили три собственных значения матрицы.
Найдем соответствующие им собственные векторы. Собственный вектор,
соответствующий собственному значению l=3, найдем из
уравнения ![]() .
.
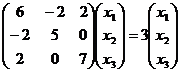 ,
,
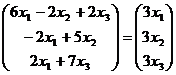 ,
,
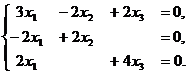
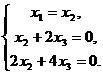
Пусть х3= -1,
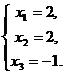 или
или 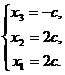
Итак, собственному значению![]() соответствует собственный вектор
соответствует собственный вектор 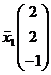 .
.
Пронормируем собственный вектор. ![]()
![]() .
.
Аналогично
находятся векторы ![]() . Базис, составленный из векторов
. Базис, составленный из векторов ![]() , является каноническим для данной квадратичной формы.
, является каноническим для данной квадратичной формы.
![]() ,
,
![]() ,
,
![]() .
.
В этом базисе квадратичная форма имеет вид ![]() .
.
Формула преобразования координат имеет вид ![]() , где
, где
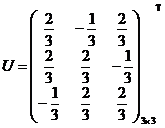 .
.