Понятие квадратичной формы
Определение 1. Скалярная функция векторного аргумента, которая представляет собой однородный многочлен второго порядка, называется квадратичной формой.
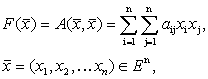
![]() R.
R.
Определение 2. Матрица, составленная из коэффициентов
квадратичной формы ![]() , называется матрицей квадратичной формы.
, называется матрицей квадратичной формы.
Пример. ![]() R,
R, ![]() .
.
![]() ,
,
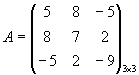 .
.
Матрица квадратичной формы
симметрична относительно главной диагонали.
Теорема 1. Любая симметричная
квадратная матрица порядка n имеет n действительных
собственных значений и собственных векторов. Собственные векторы
симметричной матрицы попарно ортогональны.
Следовательно, собственные
векторы матрицы образуют базис в пространстве
![]() .
.
Определение
3. Рангом квадратичной формы называется ранг матрицы А.
Определение 4. Квадратичная форма ![]() называется
положительно определенной (отрицательно определенной), если для любого
называется
положительно определенной (отрицательно определенной), если для любого ![]()
![]() >0 (<0).
>0 (<0).
Теорема 2 (критерий Сильвестра). Квадратичная форма является положительно
определенной тогда и только тогда, когда все левые верхние угловые миноры матрицы А являются положительными,
т.е.
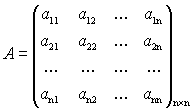 ,
,
![]() ,
,
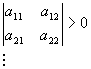 ,
,
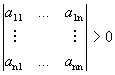 .
.