Аналитическая геометрия
Задача 1. Дан
треугольник АВС:
А(2,1), В(-1,3), С(-4,1).
Найти:
уравнение
и длину
высоты АD;
уравнение и
длину
медианы СЕ;
внутренний
угол В;
систему
линейных
неравенств,
определяющую
треугольник.
Сделать
чертеж.
Решение.
Сделаем чертеж.
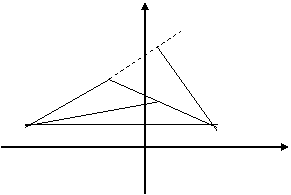 Y
Y
D
B
3
E
C 1 A
-4 -1 0 2 X
1. Составим уравнения всех сторон треугольника, используя уравнение прямой, проходящей через две данные точки.
![]() .
.
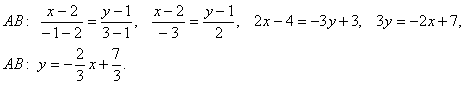
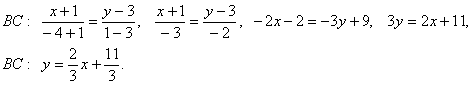
Так как
точки А и С
имеют
одинаковую
ординату,
используем
данное
уравнение в
преобразованном
виде:
![]() .
.
![]()
2. Найдем длину высоты АD. Используем формулу расстояния от точки до прямой:
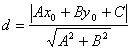 .
.
Приведем
уравнение ВС
к общему
уравнению
прямой.
![]()
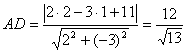 .
.
3.
Составим
уравнение
высоты АD. Она
проходит
через точку А(2,1)
и
перпендикулярна
прямой ВС, kBC=2/3. Из
условия
перпендикулярности
kAD=-1/kBC=-3/2.
Воспользуемся
уравнением
прямой, проходящей
через данную
точку в
данном
направлении:
![]() .
.
![]()
4. Для нахождения длины и уравнения медианы СЕ найдем координаты точки Е как середины отрезка АВ.
![]() Точка Е
(1/2,2).
Точка Е
(1/2,2).
![]()
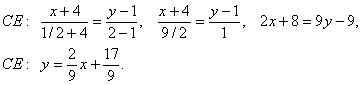
5. Найдем внутренний угол В. Он отсчитывается в положительном направлении от прямой ВС к прямой АВ. kBC=2/3, kAB=-2/3.
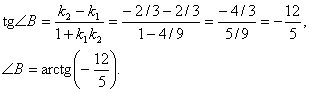
6. Составим систему линейных неравенств, определяющую треугольник. Запишем уравнения сторон в виде
AB: 2x+3y=7,
BC: 2x-3y=-11,
AC: y=1.
Подставим
точку с
координатами
(-1, 2), лежащую внутри
треугольника,
в левые части
равенств.
2x+3y=-2+6=4<7,
2x-3y=-2-6=-8>-11,
y=2>1.
Следовательно,
система
неравенств,
описывающая
треугольник,
имеет вид
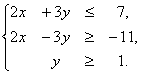
Задача
2.
Составить
каноническое
уравнение гиперболы,
если
известно, что
ее эксцентриситет
равен 1,25 и
гипербола
проходит
через точку ![]() .
.
Решение.
Каноническое
уравнение
гиперболы
имеет вид ![]() . Так как
гипербола
проходит
через точку А
(8;
. Так как
гипербола
проходит
через точку А
(8; ![]() ), то ее
координаты
удовлетворяют
уравнению гиперболы,
т.е.
), то ее
координаты
удовлетворяют
уравнению гиперболы,
т.е. ![]() .
Так, как
.
Так, как ![]() = 1,25, то
= 1,25, то ![]() = 1,25,
но
= 1,25,
но ![]() , тогда
, тогда ![]() = 1,5625
= 1,5625![]() или
или ![]() .
.
Итак,
получаем
систему двух
уравнений с
двумя
неизвестными
а и b.
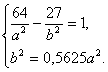
Решая
эту систему,
находим ![]() = 16 и
= 16 и ![]() = 9,
следовательно,
каноническое
уравнение
гиперболы
имеет вид
= 9,
следовательно,
каноническое
уравнение
гиперболы
имеет вид ![]() .
.
Задача
3.
Составить
уравнение
прямой,
проходящей через
вершину параболы
![]() и
центр окружности
и
центр окружности
![]() .
.
Решение.
Найдем
координаты
вершины
параболы и
координаты
центра
окружности.
Для этого
выделим
полные
квадраты по
каждой
переменной.
Уравнение
параболы: ![]() ;
;
уравнение
окружности: ![]() .
.
Следовательно,
вершина
параболы
имеет координаты
В (2;3), а центр
окружности
имеет
координаты С (-2; 1).
Тогда
уравнение
искомой
прямой
составим по
формуле
![]() .
.
Получим
![]() , или
, или ![]() .
.