Ряды

Задача. Написать три первых члена степенного ряда по заданному общему члену , определить интервал сходимости ряда и исследовать поведение ряда на концах интервала сходимости.

Решение.

При n=1 получаем .

При n=2 получаем .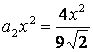

При n=3 получаем .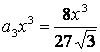

Найдем радиус сходимости ряда по формуле .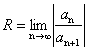

; ;

.

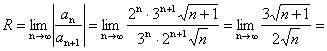
Ряд сходится при хÎ(-3/2,3/2).

Исследуем поведение ряда при , для этого в степенной ряд вместо х подставим число . Получим числовой ряд .

Для того чтобы исследовать его, сравним с гармоническим рядом . Известно, что гармонический ряд расходится. Так как при всех n, то из признака сравнения следует, что ряд также расходится.

Исследуем поведение ряда при , для этого в степенной ряд подставим . Получим числовой знакочередующийся ряд

.

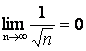Применим к нему признак Лейбница. Так как члены знакочередующегося ряда по абсолютной величине монотонно убывают и , то данный ряд сходится.

Итак, степенной ряд сходится при хÎ[-3/2,3/2).