Таблица
производных
Дифференциальное исчисление
Задача 1.
Найти
производную
функции ![]() .
.
Решение.
Преобразуем
функцию: ![]() . Тогда
. Тогда
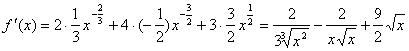 .
.
Задача 2.
Найти
производную
функции ![]() .
.
Решение. Находим
производную
сложной
функции:
![]()
![]()
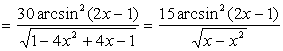 .
.
Задача 3.
Найти
производную
функции ![]() .
.
Решение.
Целесообразно
сначала
прологарифмировать
функцию:
![]() .
.
Найдем
производную
от обеих
частей
последнего
равенства:
![]() .
.
Отсюда
![]() .
.
Задача 4. С
помощью дифференциала
найти
приближенное
значение
выражения ![]() с
точностью до
0,001.
с
точностью до
0,001.
Решение.
Используем
формулу
![]() , где
, где
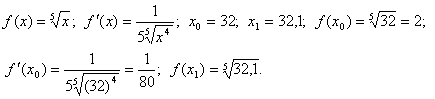
Тогда
![]() .
.
Задача 5.
Исследовать
средствами
дифференциального
исчисления
функцию ![]() и
построить ее
график.
и
построить ее
график.
Решение. 1. y=f(x).
1) Функция
определена
при всех
значениях х,
кроме х=2, т.е.
![]()
2) Четность.
![]() . Функция
не
является ни
четной, ни нечетной.
. Функция
не
является ни
четной, ни нечетной.
3) Функция
не
периодическая.
4) Найдем
точки
пересечения
графика с
осями координат.
Очевидно,
если х=0, то у=0,
и если у=0, то х=0.
Следовательно,
график
функции
проходит
через начало
координат.
5) Функция
непрерывна в
области
своего определения.
Поскольку
![]() и
и ![]() , то точка х=2
является
точкой
разрыва
второго рода.
Исследуем
поведение
функции на
бесконечности.
, то точка х=2
является
точкой
разрыва
второго рода.
Исследуем
поведение
функции на
бесконечности.
![]() .
.
6) Найдем асимптоты
графика
функции.
Известно, что
если ![]() , то прямая
, то прямая ![]() является
вертикальной
асимптотой
графика
функции. Если
является
вертикальной
асимптотой
графика
функции. Если
![]() и
и ![]() , то прямая
, то прямая ![]() является
наклонной
асимптотой
графика
функции
является
наклонной
асимптотой
графика
функции ![]() .
Поскольку
.
Поскольку ![]() и
и ![]() , то прямая х=2
является
вертикальной
асимптотой
графика
функции.
, то прямая х=2
является
вертикальной
асимптотой
графика
функции.
Найдем
![]() ; т.е. k=1.
; т.е. k=1.
![]() , т.е.
, т.е. ![]() .
.
Следовательно,
прямая ![]() является
наклонной
асимптотой
графика
функции.
является
наклонной
асимптотой
графика
функции.
2. ![]() .
.
Найдем
промежутки
монотонности
функции и
точки экстремума.
Для этого
определим ![]() .
Производная
обращается в
ноль при х=0 и 4,
а при х=2 не
существует.
.
Производная
обращается в
ноль при х=0 и 4,
а при х=2 не
существует.
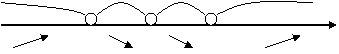
+ - - +
0 2 4 X
При ![]() ,
следовательно,
на этом
интервале
функция
возрастает.
,
следовательно,
на этом
интервале
функция
возрастает.
При ![]() функция
на этом
интервале
убывает. Следовательно,
х=0 является
точкой
максимума.
функция
на этом
интервале
убывает. Следовательно,
х=0 является
точкой
максимума.
![]() .
.
При ![]() -
убывает.
-
убывает.
При ![]() -
возрастает.
-
возрастает.
Следовательно, при х=4 функция имеет минимум:
![]() .
.
3. ![]() .
.
Определим
промежутки
выпуклости и вогнутости
графика
функции. Для
этого найдем
вторую производную:
![]() .
.
Вторая
производная ![]() на
области
определения
и не
существует
при х=2.
Исследуем
знак второй
производной.
на
области
определения
и не
существует
при х=2.
Исследуем
знак второй
производной.
![]() - +
- +
Ç 2 È X
При ![]() ,
следовательно,
в этом
интервале
график
функции
выпуклый.
,
следовательно,
в этом
интервале
график
функции
выпуклый.
При ![]() график
функции
вогнутый. Точек перегиба
график
функции не
имеет.
график
функции
вогнутый. Точек перегиба
график
функции не
имеет.
4.
График:
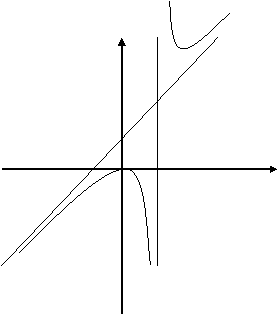
Y
8
2
-2 0 2 4
X