Исследование и построение графиков функций
Пример 1. Найти
интервалы возрастания и убывания функции
![]() .
.
Решение. Данная функция определена и дифференцируема на всей
числовой оси.
Производная функции ![]() .
.
Решаем неравенство ![]() , следовательно, функция возрастает на интервалах
, следовательно, функция возрастает на интервалах ![]() и
и ![]() . Решая неравенство
. Решая неравенство ![]() ,
, ![]() , находим
, находим ![]() . Следовательно, функция убывает на интервале
. Следовательно, функция убывает на интервале ![]() .
.
Пример 2. Найти
экстремум функции
![]() .
.
Решение. Данная функция непрерывна на всей числовой оси. Производная функции ![]() .
.
Решив уравнение ![]() , получим критическую точку
, получим критическую точку ![]() . Так как
. Так как ![]() в точке
в точке ![]() не существует, то
не существует, то ![]() тоже является критической точкой. Критическими точками
являются
тоже является критической точкой. Критическими точками
являются ![]() и
и ![]() .
.
Расположим критические точки в порядке их
возрастания на числовой оси (рис. 1)
![]()
+ -
+
0 ![]() X
X
Рис. 1
Исследуем знак производной
в окрестности каждой из этих точек при ![]() :
:
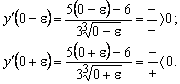
По первому достаточному условию
экстремума, при переходе через критическую точку ![]() слева направо производная
меняет знак с плюса на минус, следовательно, функция имеет в точке
слева направо производная
меняет знак с плюса на минус, следовательно, функция имеет в точке ![]() максимум, причем
максимум, причем ![]() .
.
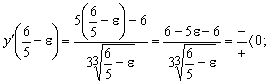
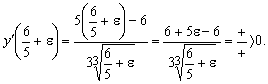
При переходе через точку ![]() производная меняет знак
с минуса на плюс, следовательно, функция имеет минимум:
производная меняет знак
с минуса на плюс, следовательно, функция имеет минимум:
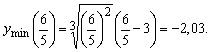
Пример 3. Найти экстремум функции ![]() на отрезке
на отрезке ![]() .
.
Решение. Данная функция определена и
непрерывна на отрезке ![]() .
.
Производная функции ![]() .
.
Решив уравнение ![]() , получим
, получим
![]() .
.
Точки ![]() являются критическими.
являются критическими.
Находим вторую производную ![]() , определим ее знак в критических точках:
, определим ее знак в критических точках:
![]() ;
; ![]() .
.
На основании второго достаточного условия
существования экстремума в точке ![]() функция имеет минимум:
функция имеет минимум:
![]() ;
;
в точке ![]() функция имеет
максимум:
функция имеет
максимум:
![]() .
.
Пример 4. Найти
интервалы выпуклости, вогнутости и точки перегиба функции
![]() .
.
Решение. Данная функция определена на всей числовой оси.
Производная функции:
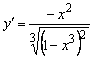 .
.
Вторая производная функции:
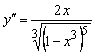 .
.
Решив уравнение ![]() , находим
, находим ![]() . Вторая производная не существует при
. Вторая производная не существует при
![]() . Критическими точками второго рода являются точки
. Критическими точками второго рода являются точки ![]() и
и ![]() .
.
Исследуем знак второй производной в
окрестности каждой из этих точек (рис. 2).
![]()
- + -
0 1 X
Рис. 2
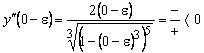 ;
;
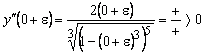 ;
;
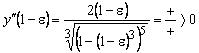 ;
;
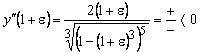 .
.
Следовательно, в промежутках ![]() функция выпукла, а в промежутке
функция выпукла, а в промежутке ![]() вогнута. При переходе
через точки
вогнута. При переходе
через точки ![]() и
и ![]() вторая производная
меняет знак, отсюда на основании достаточного условия точек перегиба эти точки
являются точками перегиба графика функции.
вторая производная
меняет знак, отсюда на основании достаточного условия точек перегиба эти точки
являются точками перегиба графика функции.
Определим значение функции в точках
перегиба:
![]() .
.
Пример 5. Найти
асимптоты графика функции ![]() .
.
Решение. Данная функция определена и непрерывна на всей
числовой оси, поэтому вертикальных асимптот график функции не имеет.
Горизонтальных асимптот функция также не имеет, так как
![]() .
.
Найдем наклонные асимптоты:

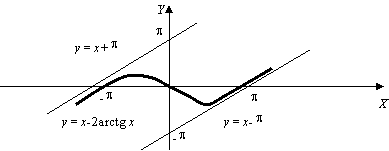
Следовательно, график функции ![]() имеет две наклонные
асимптоты
имеет две наклонные
асимптоты ![]() при
при
![]() и
и ![]() при
при ![]() .
.
График функции показан на рис. 3.
O
Рис. 3