Вариант 2

1. Найти пределы функций.

a) ; б) .

2. Найти производные заданных функций.

а) ; в) ;

б) ; г) .

3. Найти дифференциалы заданных функций.

а) ; б) .

4. Вычислить по формуле Ньютона-Лейбница определенный интеграл.

а) ; б).

5. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальному условию y=y₀ при x= x₀.

xy´- x = xe^x-1, x₀=1, y₀=0.

6. Найти частные производные первого порядка и полный дифференциал функции z=f(x,y).

z=3ctg(3x-2y).

7. Решить систему линейных уравнений двумя способами: по формулам Крамера и с помощью обратной матрицы.

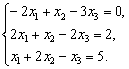
8. Найти два базисных решения системы.

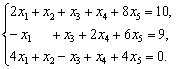
9. Решить графически задачу линейного программирования.

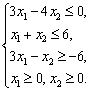
10. В ящике содержится 10 одинаковых деталей, помеченных номерами 1, 2, … , 10. На удачу извлечены 6 деталей. Найти вероятность того, что среди извлеченных деталей окажется деталь с номером 1.

11. Для случайной величины Х:

1) построить полигон распределения вероятностей;

2) составить интегральную функцию распределения и нарисовать ее график;

3) найти М(Х) – математическое ожидание, D(X) – дисперсию, δ(Х) – среднее квадратичное отклонение случайной величины Х.

Случайная величина Х задана следующим законом распределения:

x1	-2	4	5	6
p1	0,3	0,1	0,2	0,4