Применение линейной алгебры в экономике

Межотраслевой баланс производства

Пусть производственная сфера хозяйства представляет n отраслей, выпускающих однородный продукт. Процесс производства рассматривается за некоторый период времени, чаще такой единицей служит год. Продукция каждой отрасли частично предназначается на производственное потребление других отраслей, частично перерабатывается внутри отрасли. Обозначим через х_i общий (валовой) объем продукции i-й отрасли ; х_ij - объем продукции i-й отрасли, израсходованный на производственные нужды j-й отрасли ; у_i - объем продукции i-й отрасли, потребленный в той же самой отрасли , или так называемый продукт конечного потребления.

Распределение продукции каждой отрасли описывается с помощью таблицы межотраслевых связей (межотраслевого баланса):

Отрасль материального производства	Межотраслевые потоки в отрасли				Валовой выпуск отрасли	Конечный продукт n
	1	2	…	n
1	x11	x12	...	x1n	x1	у1
2	x21	x22	…	x2n	х2	у2
…	…	…	…	…	…	…
n	xn1	xn2	…	xnn	xn	уn

Балансовый принцип связи различных отраслей промышленности состоит в равенстве валового выпуска i-й отрасли и суммарного объема продукции, потребляемой n отраслями, и конечного продукта, т.е.

.

Полученные уравнения называются соотношениями баланса.

Заметим, что продукция разных отраслей имеет разные единицы измерения, поэтому будем рассматривать стоимостный межотраслевой баланс, т.е. все величины имеют стоимостное выражение.

Производство некоторого количества продукта при определенном техническом уровне требует расходования разных предметов труда. Если для производства х_j объема продукции j-й отрасли необходимо израсходовать х_ij объема продукции i-й отрасли, то на единицу продукции
j-й отрасли потребуется израсходовать

единиц продукции i-й отрасли. В. Леонтьевым на основании экономики США в 1936 г. было установлено, что технология производства в течение длительного времени остается на одном и том же уровне. Величины меняются очень незначительно и могут рассматриваться как технологические константы.

Определение. Технологическим коэффициентом производства (технологической константой) называется величина , которая определяет объем продукции i-й отрасли, необходимый для производства продукции j-й отрасли.

При таком допущении технология производства принимается линейной, а само допущение называется гипотезой линейности. При этом числа называются коэффициентами прямых затрат.

В соответствии с гипотезой линейности .

Следовательно, балансовые соотношения можно записать в виде системы уравнений:

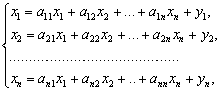
или в матричной форме ,

где Х - объем произведенной продукции (вектор валового выпуска), Y - объем продукции конечного потребления (вектор конечного потребления), А - матрица коэффициентов прямых затрат.

Определение. Соотношение называется уравнением линейного межотраслевого баланса. Вместе с описанием матричного представления это уравнение называется моделью Леонтьева.

Уравнение межотраслевого баланса позволяет решить следующие задачи:

1) найти вектор конечного продукта Y при известной матрице прямых затрат и заданном векторе валового продукта Х: ;

2) найти вектор валового выпуска Х при известной матрице прямых затрат, который обеспечивает заданный вектор конечного продукта Y: или , откуда .

Умножив обе части уравнения слева на , получим

.

Матрица

называется матрицей полных затрат.

Определение. Коэффициентами полных затрат называются величины s_ij валового выпуска продукции i-й отрасли, необходимого для обеспечения выпуска единицы конечного продукта j-й отрасли .

Заметим, что при известной матрице полных затрат А можно найти матрицу полных затрат

.

Определение. Матрица называется продуктивной, если для любого вектора существует решение уравнения . В этом случае модель Леонтьева называется продуктивной.

Заметим, что матрица А продуктивна, если для любых и

и существует номер j такой, что

.

Определение. Чистой продукцией отрасли называется разность между валовой продукцией этой отрасли и затратами продукции всех отраслей на производство данной отрасли.

Пример 1. Данные об исполнении баланса за отчетный период (усл. ден. ед.) приведены в таблице:

Отрасль производства	Потребление		Конечный продукт	Валовой продукт
	Энергетика	Машиностроение
Энергетика	7	21	72	100
Машиностроение	12	15	123	150

Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление энергетической отрасли увеличится вдвое, а у машиностроения сохранится на прежнем уровне.

Решение. Согласно данным таблицы имеем следующие показатели:

- валовой выпуск отрасли;

- объем продукции, израсходованный на производственные нужды;

- продукт конечного потребления.

Найдем по формуле

коэффициенты прямых затрат:

а₁₁=7/100=0,07, а₁₂=21/150=0,14,

а₂₁=12/100=0,12, а₂₂=15/150=0,10,

т.е.

- матрица прямых затрат, которая имеет неотрицательные элементы и удовлетворяет критерию продуктивности:

.

Поэтому для любого вектора конечного продукта Y можно найти необходимый объем валового выпуска X по формуле X=(E-A)^-1Y.

Найдем матрицу полных затрат S=(E-A)^-1:

.

Так как │E-A│=0,93∙0,90-0,12∙0,14=0,8202 ≠ 0, тогда, согласно формуле

,

.

По условию задачи, конечное потребление энергетической отрасли увеличилось вдвое, т.е. вектор конечного продукта

.

Согласно формуле получим вектор валового выпуска после изменений:

,

т.е. валовой выпуск в энергетической отрасли надо увеличить до 179,0 усл. ед., а в машиностроительной - до 160,5 усл. ед.

Пример 2. Обувная фабрика выпускает три вида изделий: сапоги, кроссовки и ботинки; при этом используется сырье трех типов: S₁, S₂, S₃. Нормы расхода каждого из них на одну пару и объем расхода сырья на 1 дн. заданы в таблице:

Вид сырья	Нормы расхода сырья на одну пару, усл. ед.			Расход сырья на 1 дн., усл. ед.
	сапоги	кроссовки	ботинки
S1	5	3	4	2700
S2	2	1	1	900
S3	3	2	2	1600

Найти ежедневный объем выпуска каждого вида обуви.

Решение. Обозначим ежедневный выпуск пар сапог - х₁, пар кроссовок - х₂, пар ботинок - х₃. Тогда в соответствии с расходом сырья каждого вида имеем систему:

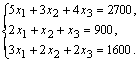
Решим систему по формулам Крамера

.

; ;

; ,

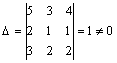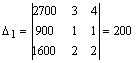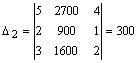откуда

, ,

Фабрика выпускает 200 пар сапог, 300 пар кроссовок, 200 пар ботинок.

Линейная модель торговли

Процесс взаимных закупок товаров анализируется с использованием понятий собственного числа и собственного вектора матрицы.

Пусть бюджеты n стран х₁, х₂, …, х_n расходуются на покупку товаров. Тогда а_ij - доля бюджета х_j, которую j-я страна тратит на закупку товаров у i-й страны. Введем матрицу коэффициентов а_ij:

.

В случае, если весь бюджет расходуется только на закупки внутри страны и вне ее (это можно трактовать как торговый бюджет), справедливо равенство

.

Определение. Матрица А, у которой сумма элементов ее любого столбца равна единице, называется структурной матрицей торговли.

Для i-й страны общая выручка от внутренней и внешней торговли выражается формулой

.

Для сбалансированной торговли необходима бездефицитность торговли каждой страны, т.е. бюджет страны не должен превышать выручки от торговли (), или .

В условиях не может быть знака неравенства, так как, сложив все эти неравенства при i от 1 до n и сгруппировав слагаемые с величинами бюджетов х_j , получим

.

Очевидно, что в скобках стоят суммы элементов матрицы А по ее столбцам, которые равны единице по условию. Имеем противоречивое неравенство , в котором возможен только знак равенства.

Следовательно, условия принимают вид равенств:

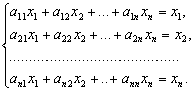
Введя вектор бюджетов , каждая компонента которого характеризует бюджет соответствующей страны, получим уравнение в матричной форме:

или .

Задача свелась к нахождению собственного вектора структурной матрицы А, отвечающего ее собственному значению .

Пример 3. Структурная матрица торговли двух стран имеет вид

.

Найти национальные доходы указанных стран для сбалансированной торговли.

Решение. Составим характеристическое уравнение для данной матрицы:

,

откуда или . Получим: , .

Найдем собственный вектор , соответствующий собственному значению при . Для этого решим матричное уравнение :

,

откуда

.

Получим .

Пусть , тогда вектор при любом является собственным вектором матрицы А с собственным значением .

Полученный результат означает, что сбалансированность торговли двух стран достигается при векторе национальных доходов , т.е. при соотношении национальных доходов стран 1:-2.