Собственные векторы и собственные значения матриц

Пусть дана квадратная матрица n-го порядка:

.

Определение. Число λ называется собственным значением квадратной матрицы А порядка n, если найдется вектор такой, что .

Определение. Вектор называется собственным вектором матрицы А, соответствующим данному собственному значению λ.

Равенство в матричной форме примет вид

или

.

Полученная однородная система уравнений всегда имеет нулевое решение . Для существования ненулевого решения необходимо и достаточно, чтобы определитель системы

,

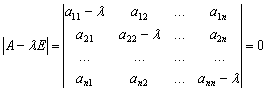где определитель является многочленом n-й степени относительно λ.

Определение. Уравнение называется характеристическим уравнением матрицы А.

Теорема. Число различных собственных значений квадратной матрицы не превосходит ее порядка. Собственные векторы, отвечающие различным собственным значениям, линейно независимы.