Применение понятия матрицы

в экономике

Данные о выпуске продукции нескольких видов в каждом квартале, нормы затрат ресурсов на производство продукции разных типов и другие параметры записываются для удобства в виде матриц, что позволяет быстро находить различные производственные показатели.

а) Пусть в некоторой отрасли m предприятий выпускают n видов продукции. Матрица задает объемы продукции на каждом предприятии в первом квартале, матрица задает объемы продукции во втором квартале; характеризуют объемы продукции j-го типа на i-м предприятии в первом и втором кварталах, соответственно.

Для определения объемов продукции за полугодие необходимо найти сумму матриц А и В.

- объем продукции j-го типа, произведенный за полугодие i-м предприятием.

Прирост объемов производства D во втором квартале по сравнению с первым по видам продукции и предприятиям определяется разностью матриц В и А:

.

Заметим, что отрицательные элементы d_ij показывают, что на данном предприятии i-й объем производства j-го продукта уменьшился; положительные d_ij показывают увеличение объемов производства j-го продукта, а нулевые d_ij означают, что объем производства не изменился.

Стоимостное выражение объемов выпущенной продукции за полгода (в условных единицах, если k - курс условной единицы по отношению к рублю) по каждому предприятию дает произведение

.

Пример 1. На четырех заводах выпускают три вида продукции. Объемы продукции на каждом заводе в первом квартале заданы матрицей А, а во втором квартале - матрицей В:

; .

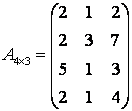Найти: 1) объемы продукции второго завода; 2) изменение во втором квартале по сравнению с первым объемов производства третьего вида продукции на четвертом заводе; 3) стоимость выпущенной продукции за полгода в долларах на первом заводе, если доллар стоит 27 руб.

Решение.

1) Объем продукции за полгода составит :

.

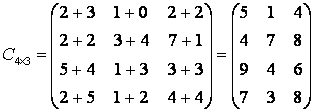Из полученной системы следует, что объем продукции второго завода по четырем видам продукции , в общем: .

2) Объем производства во втором квартале по сравнению с первым равен :

.

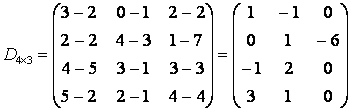Из полученной матрицы следует, что во втором квартале по сравнению с первым на четвертом заводе объемы производства третьего вида продукции не изменились, так как d₄₃=0.

3) Стоимость объемов произведенной продукции за полгода в долларах составит kС=k(А+В):

.

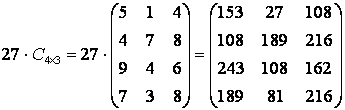Из полученной матрицы следует, что стоимость объемов продукции первого завода за полгода по четырем видам продукции , а общая стоимость составила долларов.

б) Пусть предприятие производит n видов продукции, объемы выпуска заданы матрицей . Цена реализации единицы i-го вида продукции в j-м регионе задана матрицей , где k - число регионов, в которых реализуется продукция.

Выручка за реализацию n видов продукции по регионам определяется матрицей , где

- выручка предприятия в j-м регионе:

.

Пример 2. Фирма производит три вида продукции, объемы которых заданы матрицей , в четырех городах. Цена реализации единицы продукции каждого вида по городам представлена матрицей

.

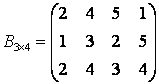Определить город, в котором фирма получает наибольшую выручку.

Решение. Выручка фирмы по городам равна :

.

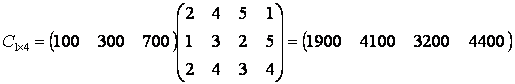Из полученной матрицы следует, что наибольшую выручку фирма получает в четвертом городе, так как ден. ед.

в) Пусть предприятие производит n типов продукции, используя m видов ресурсов. Матрица представляет нормы затрат ресурса i-го товара на производство единицы продукции j-го типа. Количество продукции каждого типа х_ij, выпущенное за определенный отрезок времени, задано матрицей .

Полный расход ресурсов каждого вида на производство всей продукции за данный период времени определяется матрицей , т.е.

.

Заметим, что если в задаче указать матрицу , задающую стоимость каждого вида ресурсов в расчете на единицу, то можно найти стоимость затраченных ресурсов: или .

.

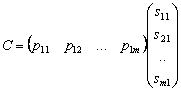Пример 3. На предприятии изготавливается три типа изделия при использовании четырех видов сырья. За полгода предприятие выпустило изделий в количестве , при этом на их производство затратило сырья

.

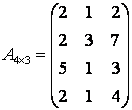Определить, какой вид сырья за данный период будет меньше израсходован.

Решение. Затраты сырья по видам изделий равны :

.

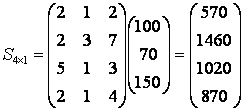Из матрицы следует, что за полгода меньше израсходуется первое сырье, так как ед. сырья.

Пример 4. Определить стоимость затрат предприятия на сырье, если стоимость каждого вида сырья в расчете на единицу представлена матрицей при общих затратах сырья на производство .

Решение. Стоимость затраченных ресурсов на производство продукции составит :

ден. ед.