3

Применение дифференциальных уравнений

в экономических исследованиях

Модель естественного роста выпуска

Пусть Q(t) количество продукции, реализованной к моменту времени t, по некоторой фиксированной цене P. Тогда доход к моменту времени t составит .

Допустим, что при условии ненасыщаемости рынка скорость выпуска продукции (акселерация) пропорциональна величине инвестиций I(t), направленных на расширении производства, т.е. , где - норма акселерации.

При инвестировании в производство фиксированной части дохода получим:

, (1)

где m - коэффициент пропорциональности - постоянная величина, .

Подставив равенство в выражение , придем к уравнению

(2)

или

. (3)

Уравнение (3) является дифференциальным уравнением с разделяющимися переменными. Его общее решение имеет вид , где С - произвольная постоянная. Если в начальный момент времени задан объем выпуска Q₀, то из этого условия можно найти С. Тогда , откуда .

Частное решение, удовлетворяющее начальным условиям, примет вид .

Заметим, что уравнение описывает также демографический процесс, динамику роста цен при постоянной инфляции и др. Кроме того, модель роста в условиях конкурентного рынка примет вид , оставаясь дифференциальным уравнением с разделяющимися переменными, так как с увеличением объема произведенной продукции ее цена падает в результате насыщения рынка.

Пример 1. Кривая спроса р(у) задается уравнением , норма акселерации , норма инвестиций m=0,5, у(0)=0,5. Найти выражение для объема реализованной продукции .

Решение. Согласно формуле уравнение примет вид или

Интегрируя, получим

или ,

где .

Зная, что у(0)=0,5, имеем

откуда С = -3.

Выражая у из

окончательно получим

Заметим, что получили функцию, график которой представляет собой логистическую кривую.

Определение. Функцией логистики (снабжения) называют функцию вида

, (4)

где значение А определяется из начальных условий.

Заметим, что данная функция получается из уравнения снабжения или логистики вида

, (5)

где p и m - постоянные.

Данное уравнение с разделяющимися переменными

Или

Интегрируя, получим

или

Из последнего равенства найдем у:

При y=m уравнение имеет вид , производная меняет знак с "+" на "-", т.е. y=m - максимальное значение, что позволяет использовать его для моделирования ограниченного роста населения.

При у<<m уравнение (k=pm) имеет решение и описывает неограниченный экспоненциальный рост населения.

Пример 2. Уравнению логистики с постоянной k=pm=0,2 соответствует рост количества бактерий в сосуде. Найти время, за которое количество бактерий достигнет 80% от максимального, если в начальный момент времени количество бактерий составляло 1% от максимально возможного значения m.

Решение. При k=pm=0,2 уравнение логистики примет вид

или .

Интегрируя с условием у<m, получим

Пользуясь начальным условием у=0,01m при t=0, найдем значение С и подставим его в решение

откуда .

Получим

или ,

откуда

- решение задачи.

Найдем t при y=0,8 m:

или ,

тогда или , откуда t=5ln396 ≈ 29,91.

Модель естественного роста дохода

Пусть Y(t) - доход, полученный к моменту времени t некоторой отраслью, является суммой инвестиций I(t) и величины потребления C(t), т.е. . (6)

Допустим, что скорость увеличения дохода пропорциональна величине инвестиций, т.е.

, (7)

где b - коэффициент капиталоемкости прироста дохода.

При потреблении фиксированной части получаемого дохода получим: , где m - норма инвестиций - постоянная величина, .

Подставив выражения и в равенство , получим уравнение:

. (8)

Данное уравнение - дифференциальное с разделяющимися переменными. Его общее решение имеет вид , где С - произвольная постоянная. Если в начальный момент времени зафиксирован доход Y₀, то из этого условия можно найти С. Тогда , откуда .

Частное решение, удовлетворяющее начальным условиям, примет вид

Пример 3. Найти функцию дохода Y = Y(t), если известно, что величина потребления задается функцией C = 2t; коэффициент капиталоемкости прироста дохода b = 1/2, Y(0) = 2.

Решение. Из соотношений и имеем уравнение

т.е. функция дохода удовлетворяет линейному однородному уравнению первого порядка.

Решение будем искать в виде уравнения , тогда получим

, ν(t)=e²^t.

Значение постоянной C найдем из условия Y(0)=2, тогда , откуда С = 1. Окончательно имеем .

Пример 4. Эластичность спроса

для любых значений р. Найти функцию спроса.

Решение. Согласно определению эластичности

получим дифференциальное уравнение с разделяющими переменными:

или .

После интегрирования получим уравнение спроса:

, откуда .

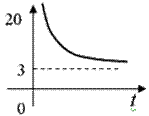
Пример 5. Найти зависимость равновесной цены от времени t, если в начальный момент времени цена р = 20, а функции спроса и предложения на некоторый товар имеют вид

, .