Применение понятия производной

в экономике

 

Производительность труда

Пусть функция  определяет количество произведенной продукции у за время t. Найти производительность труда в момент .

За период времени от t0 до  количество произведенной продукции изменится от значения  до значения . Тогда средняя производительность труда за период времени ∆t равна . Очевидно, что производительность труда в момент t0 определяется как предельное значение средней производительности за период времени от t0 до  при , т.е.

 - предельная производительность труда.    (1)

Следовательно, производительность труда есть скорость изменения количества произведенной продукции за единицу времени. Заметим, что вторая производная от количества произведенной продукции по времени является ускорением для данной функции, или скоростью для производительности труда за единицу времени.

 

Пример 1. Объем продукции, произведенной бригадой рабочих за восьмичасовую смену, описывается уравнением  единиц продукции, где t - рабочее время в часах. Вычислить производительность труда и скорость ее изменения в начале и в конце рабочего дня.

Решение. Производительность труда

;

скорость ее изменения

.

В начале рабочего дня (при t0=0) производительность труда бригады ;

скорость ее изменения .

В конце рабочего дня (при ) производительность труда бригады и скорость ее изменения получают следующие значения: , .

 

Пример 2. Объем продукции, произведенной бригадой рабочих, может быть описан уравнением

(ед.), ,

t - рабочее время в часах. Вычислить производительность труда, скорость и темп ее изменения через час после начала работы и за час до ее окончания.

Решение. Производительность труда

;

скорость изменения производительности

;

темп изменения производительности

.

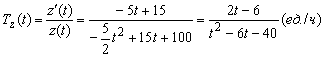В момент времени  имеем

 (ед./ч),  (ед./ч2),  (ед./ч).

В момент времени  получим

 (ед./ч),  (ед./ч2),  (ед./ч).

Итак, к концу работы производительность труда существенно снижается; при этом изменение знака  и  с плюса на минус свидетельствует о том, что увеличение производительности труда в первые часы рабочего дня сменяется ее снижением в последние часы.

 

Издержки производства и прибыль

Издержки производства C однородной продукции есть функция количества выпускаемой продукции Q, т.е. . Пусть  - увеличение количества продукции, а  - приращение издержек. Тогда среднее приращение издержек производства на единицу продукции

.

Производная

                                                 (2)

выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции.

Предельные издержки зависят от количества выпускаемой продукции и определяются переменными производственными затратами на сырье, топливо и т.п.

Аналогично находятся предельная выручка (доход)

                                    (3)

и предельная прибыль

.                                            (4)

Кроме издержек производства товара, существуют издержки его хранения.

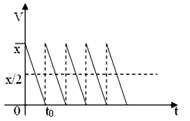
Пусть товар завозится на склад партиями по х штук в одной партии, а расходуется с постоянной скоростью. Тогда наполняемость склада зависит от времени t и задается функцией, график которой представлен на рис. 1.

 

 

 

Рис. 1

На графике V - количество товара на складе, x/2 - средняя наполняемость склада, t0 - время использования партии товара.

Издержки производства товара и издержки его хранения представляют собой совокупные издержки.

Заметим, что в экономической литературе предельные величины называют также маржинальными.

 

При их записи к обычному обозначению величин добавляется буква М; при записи средних величин добавляется буква А (от англ. Average - средняя). Например, MR - предельный доход, AR - средний доход.

 

Пример 3. Издержки производства С, зависящие от объема продукции Q, выражаются уравнением  (ден. ед.). Определить средние и предельные издержки, если объем производства составляет 10 ед. продукции.

Решение. Предельные издержки определяются выражением , откуда .

 

Средние издержки

,

откуда .

Сравнение значений средних и предельных издержек производства при выпуске 10 ед. продукции означает, что увеличение объема на 1 ед. продукции обойдется фирме приближенно в 11 ден. ед. при средних затратах на производство 1 ед. продукции 18 ден. ед.

 

Потребление и сбережение

Доход y, остающийся у населения после уплаты налогов, состоит из двух слагаемых: . Первое слагаемое  представляет собой часть доходов, которую население тратит. Эта часть составляет функцию потребления . Второе слагаемое  составляют сбережения населения. Функция  называется функцией сбережения.

Если национальный доход Y получает приращение , то функции потребления и сбережения также получают приращения, соответственно,  и : .

Разделив последнее равенство на ∆y ≠ 0, перейдем к пределу при . Получим

, т.е. .         (5)

Производная

называется предельной склонностью к потреблению, производная

 - предельная склонность к сбережению.

Заметим, что полученные предельные величины позволяют определить изменения потребления и сбережения при увеличении (уменьшении) национального дохода.

 

Пример 4. Зависимость потребления от национального дохода задается выражением . Найти предельные склонности к потреблению и сбережению при национальном доходе 30 ед.

Решение. Предельная склонность к потреблению

,

откуда

.

Предельную склонность к сбережению найдем, пользуясь равенством

.

При данном уровне национального дохода население больше склонно проедать его. Если национальный доход увеличить на 1 ед. от уровня 30, то потребление вырастет на 0,8 и только 0,2 пойдут на инвестиции.

 

Производственная функция

Производственная функция является экономико-математическим уравнением, связывающим переменные величины затрат (ресурсов) с величинами продукции (выпуска). Пусть количество продукции Q зависит только от приложенного труда L (численности персонала). Производственная функция примет вид .

Для оценки эффективности производства используется средняя производительность труда PL, которая определяется отношением .

Руководителей больше интересуют изменения объема продукции Q при увеличении (уменьшении) численности персонала. Понятие предельной производительности труда как производной от продукции Q по величине приложенного труда L позволяет получить ответ, т.е. .                                                                        (1.14)

Предельная производительность приближенно равна изменению объема выпускаемой продукции при изменении численности персонала на единицу.

 

Пример 5. Производственная функция задана в виде

. Определить влияние численности персонала на объем выпускаемой продукции.

Решение. Предельная производительность труда

.

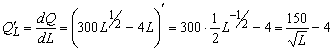Подставим в полученную формулу значения L: ; ; ; ;  (значения L заданы произвольно).

Получим:

;        ;           ;                   ;        .

;    ;        ;                   ;         .

Из полученных результатов видно, что предельная производительность труда уменьшается с ростом численности персонала. Значит, при дальнейшем увеличении персонала производство продукции будет падать, так как исполнители одного и того же дела начинают мешать друг другу.