Задачи для самостоятельной работы

Блок 1

1. Функция потребления некоторой страны имеет вид: , где - совокупный национальный доход (ден. ед.). Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 27 ден. ед.

2. Объем производства осенней обуви , выпускаемой некоторой фирмой, может быть описан уравнением (ед.), где - календарный месяц года. Найти производительность труда, скорость и темп ее изменения: а) в начале года ; б) в середине года ; в) в конце года .

3. Зависимость между издержками производства и объемом выпускаемой продукции на предприятии выражается функцией . Определить средние и предельные издержки при объеме продукции 10 ед.

4. Выручка от продажи макаронных изделий составляет , где - объем проданной продукции (тыс. ед.). Найти среднюю и предельную выручку, если продано: а) 10 тыс. ед., б) 60 тыс. ед.

5. Функция издержек производства от объема выпускаемой продукции имеет вид . Определить средние и предельные издержки при объеме продукции 10 ед.

6. Себестоимость продукции связана с объемом выпускаемой продукции уравнением: . Определить среднюю и предельную себестоимость выпускаемой продукции при объеме, равном 10 ед.

7. Производительность труда бригады может быть описана уравнением , где - рабочее время в часах. Вычислить скорость и темп изменения производительности труда при и .

8. Себестоимость производства бытовой техники (в тыс. руб.) описывается функцией , , где - объем выпускаемой продукции в месяц (тыс. ед.). Определить скорость и темп изменения себестоимости при выпуске 20 и 40 тыс. ед. продукции.

9. Функция потребления некоторой страны имеет вид , где - совокупный национальный доход. Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 32.

10. Функция сбережения некоторой страны имеет вид , где - совокупный национальный доход. Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 27.

11. Зависимость между себестоимостью готовой продукции предприятия (млн. руб.) и объемом выпускаемых изделий (тыс. руб.) выражается уравнением . Найти эластичность себестоимости продукции предприятия, выпускающего 12 тыс. шт. изделий. Какие рекомендации можно дать руководителям предприятий об изменении величины объема выпускаемой продукции?

12. Функция полных затрат в зависимости от объема выпускаемой продукции задана соотношением . При каком объеме производства предельные и средние затраты совпадают? Найти коэффициенты эластичности полных и средних затрат при данном объеме.

13. Зависимость между объемом выпуска готовой продукции (млн. руб.) и объемом производственных фондов (млн. руб.) выражается уравнением . Найти эластичность выпуска продукции для предприятия, имеющего фонды в размере 40 млн. руб.

14. Зависимость между себестоимостью единицы продукции (в руб.) и выпуском продукции (в млн. руб.) выражается уравнением . Найти эластичность себестоимости при выпуске продукции на 30 млн. руб.

15. Зависимость между количеством выпускаемых деталей в партии (тыс. ед.) и затратами на их изготовление (тыс. руб.) для предприятий отрасли выражается уравнением . Найти эластичность затрат для предприятий, выпускающих по 10 тыс. деталей в партии.

16. Заданы функции спроса и предложения от цены
: Найти: а) равновесную цену; б) эластичность спроса и предложения для равновесной цены; в) изменение дохода при изменении равновесной цены на 5%.

17. Функции спроса и предложения на некоторый товар от его цены задаются уравнениями: Найти: а) равновесную цену; б) эластичность спроса и предложения для равновесной цены; в) изменение дохода при изменении равновесной цены на 5%.

18. Объем продаж видеомагнитофонов задается следующей функцией времени: где - время, измеряемое в месяцах; - количество видеомагнитофонов, проданных за месяц. Найти скорость изменения объема продаж в момент времени: а) ; б) ; в)

19. Население некоторой страны растет по следующему закону: где время измеряется в годах. Найти скорость изменения населения в момент времени: а) ; б) ; в)

20. Эпидемия медленно распространяется среди населения. Число заболевших определяется формулой 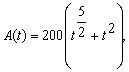где - число недель, прошедших с момента начала эпидемии. Найти скорость изменения числа заболевших в момент времени: а) ; б) ; в)

21. Предположим, что издержки получения питьевой воды заданы формулой где - процентное содержание примесей, загрязняющих воду. Найти скорость изменения издержек производства, если примеси составляют 5%.

22. Предположим, что спрос на некоторую продукцию зависит от цены следующим образом: Найти скорость изменения спроса, если цена равна: а) 10 усл. ед.; б) 25 усл. ед.

23. Издержки удаления процентов загрязнений из использованной воды равны Найти скорость изменения издержек в точке

3

24. Спрос на некоторый товар зависит от цены следующим образом: Найти скорость изменения спроса, если цена равна: а) 100; б) 16.

25. Выручка от оптовой продажи радиоприемников определяется функцией где - число проданных радиоприемников. Найти предельную выручку, если продано:
а) 100 радиоприемников; б) 200 радиоприемников.

26. Объем продукции и (усл. ед.) цеха в течение рабочего дня представляет функцию u=-t³-5t²+75t+425, где t - время (ч). Найти производительность труда через 2 ч после начала работы.

27. Зависимость между издержками производства у (ден. ед.) и объемом выпускаемой продукции х (ед.) выражается функцией
у = 10х-0,04х³. Определить средние и предельные издержки при объеме продукции, равном 5 ед.

28. Функции спроса q и предложения s от цены p выражаются, соответственно, уравнениями q = 7 - p и s = p + 1. Найти: а) равновесную цену; б) эластичность спроса и предложения для этой цены; в) изменение дохода в процентах при увеличении цены на 5% от равновесной.

29. Уравнение спроса имеет вид . Найти эластичность и выяснить, как повлияет увеличение цены на выручку, если спрос составляет: а) 150 единиц; б) 50 единиц.

30. Уравнение спроса имеет вид . Найти эластичность и выяснить, как повлияет увеличение цены на выручку, если спрос составляет: а) 24 ед.; б) 15 ед.