Экономическое содержание симплексных преобразованиЙ

Пример 1.

Рассмотрим задачу о прибыли. Для изготовления различных изделий А, В и С предприятие использует три различных вида сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия А, В и С, а также общее количество сырья каждого вида, которое может быть использовано предприятием, приведены в таблице 1.

Таблица 1

Вид сырья	Нормы затрат сырья (кг) на одно изделие			Общее количество сырья (кг)
	А	В	С
I	18	15	12	360
II	6	4	8	192
III	5	3	3	180
Цена одного изделия (руб.)	9	10	16

Изделия А, В и С могут производиться в любых количествах (сбыт обеспечен), но производство ограничено выделенным предприятию сырьем каждого вида.

Требуется составить план производства изделий, при котором общая стоимость всей произведенной предприятием продукции является максимальной.

Решение.

Составим математическую модель задачи. Искомый объем выпуска изделий А обозначим через , изделий В – через , изделий С – через . Поскольку имеются ограничения на выделенный предприятию фонд сырья каждого вида, переменные , , должны удовлетворять следующей системе неравенств:

.

(1)

Общая стоимость произведенной предприятием продукции при условии выпуска изделий А, изделий В и изделий С составляет

.

(2)

По своему экономическому содержанию переменные , и могут принимать лишь неотрицательные значения:

, , .

(3)

Таким образом, приходим к следующей математической задаче: среди всех неотрицательных решений системы (1) требуется найти такое, при котором функция (2) принимает максимальное значение.

От ограничений–неравенств в системе (1) перейдем к ограничениям–равенствам. Для этого введем три дополнительные неотрицательные переменные , в результате чего ограничения запишутся в виде системы уравнений:

.

(4)

Эти дополнительные переменные по экономическому смыслу означают не используемое при данном плане производства количество сырья того или иного вида. Например, - это неиспользуемое количество сырья I вида.

Теперь полученная математическая задача может быть переформулирована таким образом:

среди всех неотрицательных решений , , , системы линейных уравнений (4) найти такое, при котором линейная функция (2) принимает наибольшее значение.

Такая задача называется основной задачей линейного программирования, специального раздела математики, в котором, в частности, доказывается, что экстремальное значение линейной функции (2) достигается не на произвольном неотрицательном решении системы (22), а обязательно на одном из ее опорных решений (если оно вообще достигается).

Поэтому, найдя все опорные решения системы (4), вычислив на каждом из них значение функции (2) и выбрав то опорное решение, которому соответствует наибольшее из полученных чисел, мы решим исходную задачу – определим оптимальный план производства.

Заметим, что в курсе линейного программирования рассматриваются специальные методы, позволяющие сократить вычисления: отыскивать не обязательно все опорные решения, а лишь те, которые обеспечивают последовательное улучшение плана производства (последовательное возрастание значений функции (2)).

Как и ранее, будем искать опорные решения системы (4) в таблицах Гаусса, используя симплексные преобразования.

№ итерации	i	Базис
Исходная система	1		18	15	12	1	0	0	360	30
	2		6	4	8	0	1	0	192	24
	3		5	3	3	0	0	1	180	60

Так как система (4) уже приведена к единичному базису (главные переменные ), то исходное опорное решение (и исходный опорный план производства) .

Найденные значения переменных соответствуют такому "плану", при котором ничего не производится (= = = 0), сырье не используется (, , ) и значение целевой функции (2) равно нулю (т.е. стоимость произведенной продукции отсутствует): (руб.).

Введем в базис переменную , так как с экономической точки зрения наиболее целесообразным является включение в план производства изделия С: при включении в план производства одного изделия С выпуск продукции увеличивается на 16 руб., для изделия А – на 9 руб., для изделия В – на 10 руб. Найдем переменную, подлежащую исключению из базиса. Для этого по формуле симплексных преобразований находим число

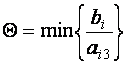
для , т.е.

.

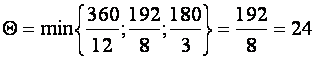Найдя число , мы тем самым с экономической точки зрения определили, какое количество изделий С предприятие может изготовлять с учетом норм расхода и имеющихся объемов сырья каждого вида. Так как сырья данного вида соответственно имеется 360, 192 и 180 кг, а на одно изделие С требуется затратить сырья каждого вида соответственно 12, 8 и 3 кг, то максимальное число изделий С, которое может быть изготовлено предприятием, равно

,

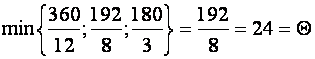т.е. ограничивающим фактором для производства изделий С является имеющийся объем сырья II вида. С учетом его наличия предприятие может изготовить 24 изделия С. При этом сырье II вида будет полностью использовано.

Следовательно, исключению из базиса подлежит переменная . Составляем таблицу I итерации.

№ итерации	i	Базис
I	1		9	9	0	1	-	0	72	8
	2				1	0		0	24	48
	3				0	0	-	1	108	72

Новый опорный план . При этом плане производства изготовляются 24 изделия С и остается неиспользованным 74 кг сырья I вида и 108 кг сырья III вида. Стоимость всей производимой при этом плане продукции равна 384 руб. , т.е. .

Более сложный (по сравнению с проведенным выше) экономический анализ таблицы I итерации (мы его не приводим) свидетельствует о том, что план не является оптимальным и следует в новый план включить производство изделия В, т.е. в базис следует ввести переменную .

При определении возможного числа производства изделий В следует учитывать имеющийся объем сырья каждого вида, а именно: возможный выпуск изделия В определяется числом

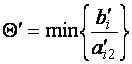
для , т.е.

.

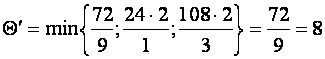Следовательно, исключению из базиса подлежит переменная , иными словами, выпуск изделия В ограничен имеющимся в распоряжении предприятия сырьем I вида. С учетом имеющихся объемов этого сырья предприятию следует изготовить 8 изделий В.

Составляем таблицу II итерации.

№ итерации	i	Базис
II	1		1	1	0		-	0	8
	2			0	1	-		0	20
	3			0	0	-	-	1	96

Ей соответствует опорный план . При этом плане производства изготовляются 8 изделий В и 20 изделий С (изделие А не производится); сырье I и II видов используется полностью и остается неиспользованным 96 кг сырья III вида; стоимость производимой продукции равна 400 руб. , т.е. .

Экономический анализ таблицы II итерации (который мы здесь не приводим ввиду его сложности) показывает, что план является оптимальным планом производства.

Ответ: , .

Заметим, что нашей целью являлось не столько обсуждение поставленной экономической задачи и ее решение (которое мы провели достаточно схематично и в урезанном виде), а экономическое истолкование условия (9) в симплексных преобразованиях, которое представляет собой, например, ограничение возможного производства определенного изделия имеющимися объемами сырья (или другого вида ресурсов).
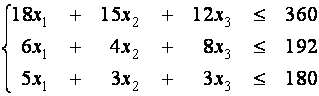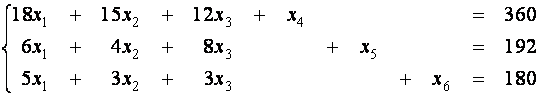