Системы линейных уравнений с невырожденной

матрицей и их решение матричным способом и по

формулам Крамера

Пусть дана система линейных уравнений

.

(1)

с матрицей размера .

.

(2)

Введем еще две матрицы:

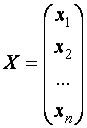- матрица-столбец из неизвестных ;

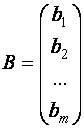- матрица-столбец из свободных членов .

Используя правило умножения матриц и условие равенства двух матриц, можем систему (1) записать в виде одного матричного уравнения

.

(3)

Про формулу (3) принято говорить, что она задает систему линейных уравнений (1) в матричной форме.

Решить матричное уравнение (3) означает найти матрицу по известным матрицам и .

Эта задача сравнительно легко решается (причем единственным образом) в случае невырожденной (квадратной) матрицы и произвольной матрицы - столбца .

Заметим, что умножение матриц, не обладая, вообще говоря, переместительным свойством, обладает свойством сочетательным, т.е. .

Умножая обе части уравнения (3) на матрицу слева ( существует, т.к. - невырожденная матрица), получим матричное равенство

.

Учитывая, что (по сочетательному свойству умножения матриц), (для любой допустимой матрицы ), получим

.

(4)

Убедимся простой подстановкой, что формула (17) действительно дает решение матричного уравнения (16):

.

Нахождение решения системы (1) в случае невырожденной матрицы с помощью формулы (4) называется матричным способом ее решения.

Заметим, что в этом случае система (1) совместна и определенна.

Пример 1. Решите матричным способом систему уравнений

.

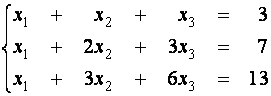Решение.

Матрица системы

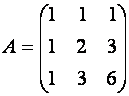
невырожденная, так как , и ее обратная матрица

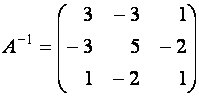
, столбец свободных членов

,

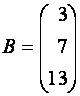и тогда по формуле (4)

.

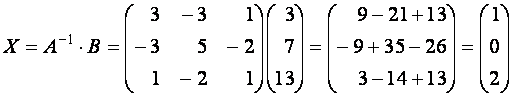Так как

,

то , или, в векторной форме,

Ответ: или

Матричную форму (4) записи решения системы (1) заменим на формул для каждой из неизвестных следующим образом:

= =

= ,

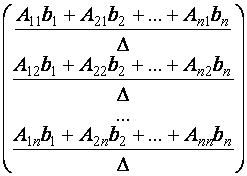откуда с учетом условия равенства двух матриц находим:

.

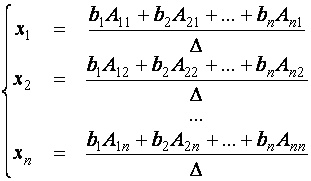Так как (согласно свойству 9 определителя) выражение

представляет собой разложение по элементам первого столбца определителя

,

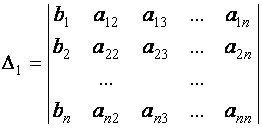выражение

-

разложение по элементам второго столбца определителя

, …,

а выражение

-

разложение по элементам -го столбца определителя

,

окончательно получим:

.

(5)

Формулы (5) найдены известным швейцарским математиком Габриелем Крамером (1704- 1752), опубликованы в 1750г. и называются в его честь формулами Крамера.

Заметим, что каждый определитель , где , получается из определителя матрицы системы заменой в нем -го столбца столбцом свободных членов.

Таким образом, система линейных уравнений с невырожденной матрицей совместна и определенна при любом столбце свободных членов и ее решение может быть найдено либо матричным способом по формуле (4), либо по формулам Крамера (5).

Пример 2. Решите систему линейных уравнений

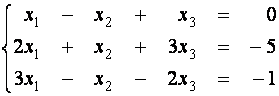
двумя способами: по формулам Крамера и с помощью обратной матрицы.

Решение.

Запишем матрицу системы

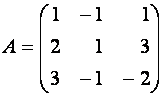
и вычислим ее определитель

= = .

Так как , то матрица невырожденная и система имеет единственное решение.

1) По формулам Крамера:

.

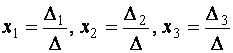Вычислим определители:

= = ;

= = ;

= = .

Тогда .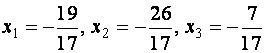

Для проверки вычислений подставим найденные значения неизвестных в систему:

,

,

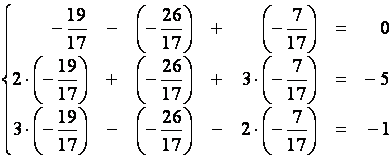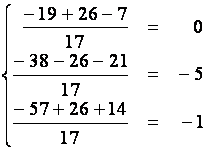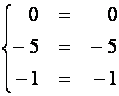
- истинные числовые равенства.

Итак,

.

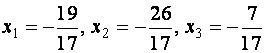2) С помощью обратной матрицы решение находим по формуле

, где

, ,

.

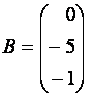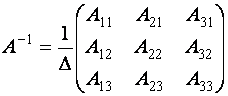Остается вычислить алгебраические дополнения:

, ,

, ,

, ,

, ,

.

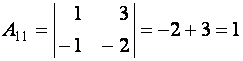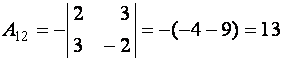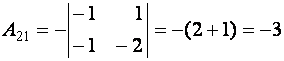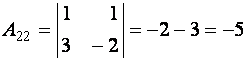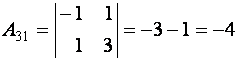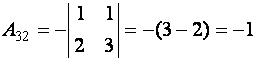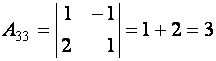Тогда

.

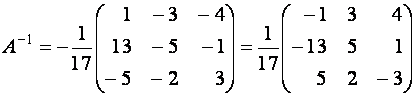Для проверки вычислений найдем произведение

=

.

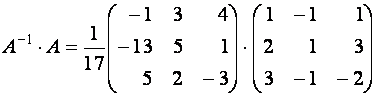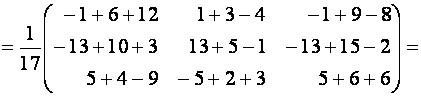
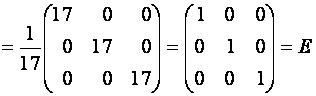Теперь

,

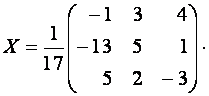
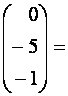
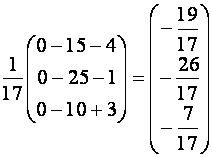откуда

.

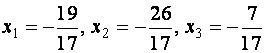Результаты по обоим методам решения совпали.

Ответ:

.
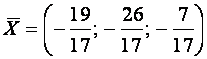
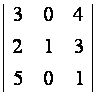
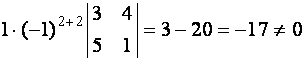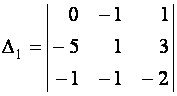
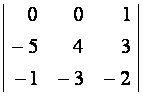
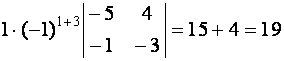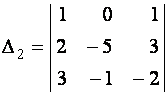
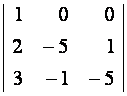
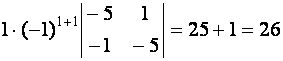
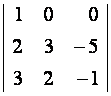
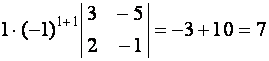