определители
Мы уже связали с каждой матрицей ![]() размера
размера ![]() целое число
целое число ![]() - ее ранг, равный
числу строк ступенчатой матрицы
- ее ранг, равный
числу строк ступенчатой матрицы ![]() , эквивалентной данной матрице
, эквивалентной данной матрице ![]() , т.е. полученной из матрицы
, т.е. полученной из матрицы ![]() с помощью элементарных
преобразований ее строк. При этом
с помощью элементарных
преобразований ее строк. При этом ![]() , где
, где ![]() .
.
Ранг
![]() для нулевой матрицы
(все элементы которой равны нулю). Для квадратной матрицы порядка
для нулевой матрицы
(все элементы которой равны нулю). Для квадратной матрицы порядка ![]() справедливы
неравенства
справедливы
неравенства ![]() . Если
. Если ![]() , то мы уже называли такую квадратную матрицу невырожденной.
, то мы уже называли такую квадратную матрицу невырожденной.
Примерами
невырожденных матриц могут служить единичные матрицы произвольного порядка,
треугольные (в частности, диагональные) матрицы без нулей на главной диагонали. Если же в треугольной (диагональной) матрице на главной
диагонали есть хотя бы один нулевой элемент, то она, очевидно, является вырожденной.
Поставим
теперь в соответствие каждой квадратной матрице еще одно число (не обязательно
целое) – определитель матрицы, или
просто определитель.
Назовем
определителем (или детерминантом)
треугольной (диагональной) матрицы произведение элементов ее главной диагонали. Будем для определителя
использовать обозначения ![]() или
или ![]() .
.
Тогда
для единичной матрицы ![]() любого порядка
любого порядка ![]() . Для треугольной матрицы
. Для треугольной матрицы
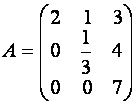
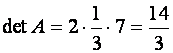 .
.
Для
произвольной квадратной матрицы ![]() введем понятие
определителя следующим образом:
введем понятие
определителя следующим образом: ![]() , где
, где ![]() - треугольная матрица,
полученная из матрицы
- треугольная матрица,
полученная из матрицы ![]() с помощью элементарных
преобразований строк (столбцов) только
одного типа (третьего): прибавление к одной строке другой строки,
умноженной на число, отличное от нуля.
с помощью элементарных
преобразований строк (столбцов) только
одного типа (третьего): прибавление к одной строке другой строки,
умноженной на число, отличное от нуля.
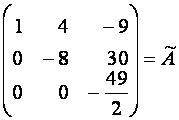
Пример 1. Вычислите определитель матрицы
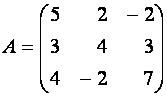 .
.
Решение.
|
|
|
~ |
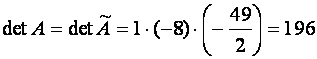 .
.
Ответ: ![]() .
.
Заметим, что для матрицы 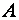 , имеющей нулевой столбец (нулевую строку), ее определитель
, имеющей нулевой столбец (нулевую строку), ее определитель 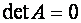 , так как после приведения ее к треугольному виду
, так как после приведения ее к треугольному виду  только с помощью указанного вида элементарных преобразований строк
(столбцов) ее главная диагональ
обязательно будет содержать хотя бы один нулевой элемент. Дело в том, что весь
нулевой столбец (нулевая строка) сохранится в матрице
только с помощью указанного вида элементарных преобразований строк
(столбцов) ее главная диагональ
обязательно будет содержать хотя бы один нулевой элемент. Дело в том, что весь
нулевой столбец (нулевая строка) сохранится в матрице  .
.
Выведем формулы для вычисления детерминанта произвольной матрицы второго и третьего порядков по ее исходным элементам, а затем с помощью полученных формул обсудим общие свойства определителей.
Пусть
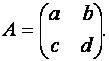
1)
Если ![]() , то
, то
|
|
|
и
|
Таким образом
при ![]()
|
|
(1) |
2)
Если ![]() ,
, ![]() , то
, то
|
|
|
|
и формула (1) сохраняется и в этом случае.
3)
Если ![]() ,
, ![]() , то
, то ![]() (матрица
(матрица ![]() содержит нулевой столбец). С другой стороны,
содержит нулевой столбец). С другой стороны, 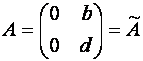 ,
,![]() .
.
По формуле (I0) получили бы тот же
результат: 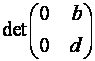 =
=![]() .
.
Итак, формула (I0) верна для определителя любой матрицы второго порядка.
Пусть теперь 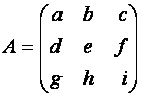 .
.
Без ограничения общности
можем считать ![]() (в противном случае
поступим как в пункте 2) или 3) для определителя матрицы второго порядка).
(в противном случае
поступим как в пункте 2) или 3) для определителя матрицы второго порядка).
![]()
![]() Тогда
Тогда
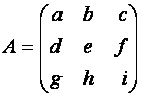
![]()
![]() ~
~  .
.
1)
Сначала рассмотрим случай ![]() .
.
Тогда
![]() ~
~ 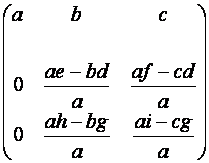
 ~
~
~  ,
,
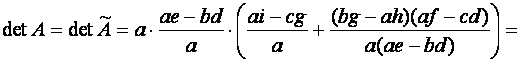
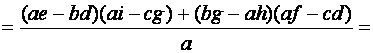
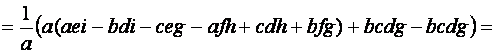
![]() .
.
Таким образом, при ![]() ,
, ![]()
|
|
(2) |
2)
Пусть теперь ![]() , но
, но ![]() .
.
Тогда
![]() ~
~  ~
~
![]()
![]() ~
~ 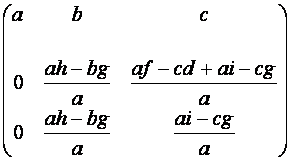
![]() ~
~
~ 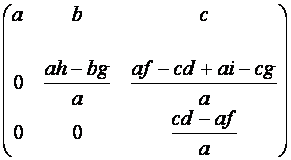
![]()
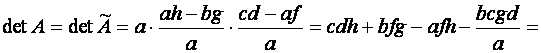
![]() т.к.
т.к. ![]()
![]() .
.
Получена та же формула (2), что и в случае 1).
3) Пусть теперь ![]() и
и ![]() . В этом случае
. В этом случае
![]() ~
~ 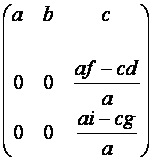
![]()
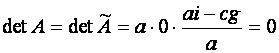 .
.
Легко проверяется справедливость формулы (2) и в этом случае.
Итак, для определителя матрицы третьего порядка (или короче, для определителя третьего порядка) справедлива формула
|
|
(2) |
Из формул (1) и (2) легко следует равенство
![]()
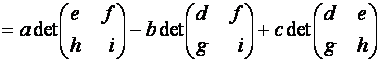 ,
,
правая часть которого представляет собой алгебраическую сумму
произведений элементов первой строки на некоторые определители матриц второго порядка,
состоящих из элементов остальных строк (второй и третьей) матрицы ![]() с сохранением их
расположения.
с сохранением их
расположения.
Каждая такая матрица может
быть получена из матрицы ![]() вычеркиванием первой строки
и одного из столбцов (первого, второго, третьего), а их определители называются
минорами элементов первой строки матрицы
вычеркиванием первой строки
и одного из столбцов (первого, второго, третьего), а их определители называются
минорами элементов первой строки матрицы ![]() или минорами элементов первой строки ее определителя.
или минорами элементов первой строки ее определителя.
Если, как обычно, элементы
матрицы ![]() обозначить
обозначить ![]() , а соответствующие им миноры -
, а соответствующие им миноры - ![]() , то полученное равенство примет вид:
, то полученное равенство примет вид:
![]()
|
или |
|
(3) |
где число ![]() называется алгебраическим дополнением элемента
называется алгебраическим дополнением элемента ![]() матрицы
матрицы ![]() .
.
Принято говорить, что формула (12) представляет собой разложение определителя третьего порядка по элементам первой строки.
Точно так же читатель может получить аналогичные формулы разложения определителя третьего порядка по элементам второй и третьей строки и по элементам любого столбца. Например, в случае второго столбца формула разложения имеет вид:
![]() .
.
Для произвольной (![]() -й) строки и произвольного (
-й) строки и произвольного (![]() -ого) столбца
соответствующие разложения имеют вид:
-ого) столбца
соответствующие разложения имеют вид:
|
где |
(4) |
Пусть теперь ![]() - произвольная квадратная
матрица порядка
- произвольная квадратная
матрица порядка ![]() :
: ![]() , здесь
, здесь ![]() - номер строки,
- номер строки, ![]() - номер столбца.
- номер столбца.
Матрица ![]() , у которой произвольный
(
, у которой произвольный
(![]() -й) столбец совпадает
с соответствующей (
-й) столбец совпадает
с соответствующей (![]() -й)
строкой матрицы
-й)
строкой матрицы ![]() , называется транспонированной к
матрице
, называется транспонированной к
матрице ![]() . Следовательно, если
. Следовательно, если ![]() ,
, ![]() , то
, то ![]() .
.
Заметим, что понятие транспонированной матрицы может быть введено для произвольной матрицы (не обязательно квадратной).
Так, например, для
матрицы
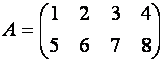
транспонированная
матрица имеет вид
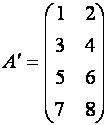 .
.
Как и выше, определитель квадратной матрицы порядка ![]() , полученной из матрицы
, полученной из матрицы ![]() вычеркиванием
вычеркиванием ![]() -ой строки и
-ой строки и ![]() -го столбца, назовем минором
-го столбца, назовем минором
![]() элемента
элемента ![]() , а величину
, а величину ![]() алгебраическим дополнением элемента
алгебраическим дополнением элемента
![]() матрицы
матрицы ![]() .
.
Для краткости вместо выражения "определитель матрицы" часто говорят просто "определитель" , используя при этом следующие обозначения:
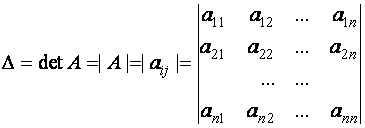 .
.
Определитель обладает следующими свойствами:
1.
Определитель не меняется при транспонировании, т.е. при
замене его строк соответствующими
столбцами и наоборот: ![]() .
.
2. При перестановке местами любых двух строк (столбцов) определитель лишь меняет знак.
3. Определитель, имеющий две одинаковые строки (столбца), равен нулю.
4. Определитель, имеющий нулевую строку (столбец), равен нулю.
5.
Если все элементы некоторой строки (столбца) определителя
умножить на некоторое число ![]() , то сам определитель умножается на
, то сам определитель умножается на ![]() .
.
5'. Общий множитель всех элементов некоторой строки (столбца) можно вынести за знак определителя.
6. Определитель, имеющий две пропорциональные строки (столбца), равен нулю.
7.
Если все элементы ![]() -й строки определителя
представлены в виде суммы двух слагаемых
-й строки определителя
представлены в виде суммы двух слагаемых
![]() ,
, ![]() ,
,
то определитель равен
сумме двух определителей, у
которых все строки, кроме ![]() -й, такие же, как и в
исходном определителе, а
-й, такие же, как и в
исходном определителе, а ![]() -я строка в одном из слагаемых определителей состоит из
элементов
-я строка в одном из слагаемых определителей состоит из
элементов ![]() , в другом – из
элементов
, в другом – из
элементов ![]() .
.
Аналогичное свойство имеет место и для столбцов определителя.
8. Определитель не изменится, если к какой-либо строке (столбцу) прибавить другую строку (столбец), умноженную на любое число.
9. Определитель равен сумме произведений элементов произвольной его строки (столбца) на их алгебраические дополнения:
|
|
|
(5) |
10. Сумма попарных произведений элементов какой-либо строки (столбца) на алгебраические дополнения элементов другой ("чужой") строки (столбца) равна нулю:
|
|
|
Перечисленные свойства легко могут быть проверены читателем для определителей второго и третьего порядков с использованием формул (1) и (2), что мы частично уже сделали.
Обратим внимание на свойство 8. Это единственное из элементарных преобразований строк (столбцов) матрицы было положено нами в основу понятия определителя, и только оно сохраняет его величину: согласно свойству 2 при перестановке любых двух строк (столбцов) определитель, вообще говоря, меняет свое значение; то же самое происходит (согласно свойству 5) при умножении строки (столбца) определителя на некоторое число; выбрасывание же нулевой строки (столбца) нарушает размер матрицы – она перестает быть квадратной.
Отметим также, что матрицы ![]() и
и ![]() имеют одинаковые
ранги, так как они эквивалентны (
имеют одинаковые
ранги, так как они эквивалентны (![]() получается из
получается из ![]() с
помощью элементарных преобразований, хотя и одного вида), и если матрица
с
помощью элементарных преобразований, хотя и одного вида), и если матрица ![]() вырожденная, т.е.
вырожденная, т.е. ![]() , то матрица
, то матрица ![]() содержит нулевую
строку
содержит нулевую
строку ![]() и поэтому
и поэтому ![]() .
.
Верно и противоположное
утверждение: если матрица ![]() невырожденная, т.е.
невырожденная, т.е. ![]() , то на главной диагонали матрицы
, то на главной диагонали матрицы ![]() нет нулевых элементов
(
нет нулевых элементов
(![]() ), и поэтому
), и поэтому ![]() . Таким образом, матрица
. Таким образом, матрица ![]() является вырожденной тогда и только тогда , если ее определитель
равен нулю (
является вырожденной тогда и только тогда , если ее определитель
равен нулю (![]() ).
).
Интересно отметить, что и при
всех остальных элементарных преобразованиях строк (столбцов) невырожденной
матрицы ![]() (очевидно, кроме
выбрасывания нулевой строки (столбца)) ее определитель, хотя и изменяет свои
значения, но не обращается в ноль (что следует из свойств 2 и 5 определителя).
(очевидно, кроме
выбрасывания нулевой строки (столбца)) ее определитель, хотя и изменяет свои
значения, но не обращается в ноль (что следует из свойств 2 и 5 определителя).
Заметим, что формулы (5),
обобщающие выведенные нами формулы (4), могут быть приняты за индуктивные
определения детерминанта произвольного порядка ![]() через детерминанты порядка
через детерминанты порядка ![]() (на единицу ниже).
Так, для вычисления определителя четвертого порядка по одной из формул (5)
потребуется вычислить четыре определителя третьего порядка. Если при этом
воспользоваться формулой (2), то это
приведет к довольно утомительным
вычислениям. А что будет, если потребуется вычислить определитель более
высокого порядка, например, седьмого?
(на единицу ниже).
Так, для вычисления определителя четвертого порядка по одной из формул (5)
потребуется вычислить четыре определителя третьего порядка. Если при этом
воспользоваться формулой (2), то это
приведет к довольно утомительным
вычислениям. А что будет, если потребуется вычислить определитель более
высокого порядка, например, седьмого?
Конечно, если некоторые элементы строки (столбца), к которой мы применяем свойство 9, окажутся нулями, то нет необходимости вычислять соответствующие им миноры.
Поэтому практичнее, не отказываясь от применения свойства 9 (формулы (5)), использовать свойство 8 для создания в какой-либо строке (столбце) возможно большего числа нулей.
Пример 2. Вычислите разложением по элементам третьей строки определитель четвертого порядка
 .
.
Решение.
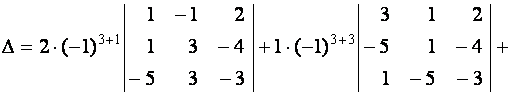

![]()
![]()
![]()
![]()
![]()
![]() .
.
Вычисление определителей третьего порядка производилось по формуле (2).
Ответ:![]() .
.
Пример 3. Вычислите, используя свойство 8, определитель предыдущего примера.
Решение.
|
|
|
|
|
|
Ответ: ![]() .
.
Пример 4. Вычислите определитель шестого порядка
 .
.
Решение.
По свойству 6 определитель равен нулю, так как его первый и шестой столбцы пропорциональны.
Ответ: ![]() .
.
Пример 5. Вычислите определитель пятого порядка
 .
.
Решение.
|
|
|
= |
|
= |
|
|
|
= |
|
|
Ответ: ![]() .
.
Заметим, что при решении примера 33 мы еще использовали свойство 5' определителя.
Используя свойства определителей, рассмотрим теперь еще один способ получения обратной матрицы.
Для произвольной
квадратной матрицы ![]() порядка
порядка ![]() введем понятие присоединенной матрицы
введем понятие присоединенной матрицы
 ,
,
элементами которой являются алгебраические дополнения
соответствующих элементов матрицы ![]() , транспонированной к матрице
, транспонированной к матрице ![]() :
:
![]() .
.
Считаем матрицу ![]() невырожденной, т.е.
невырожденной, т.е. ![]() , так как в противном случае, как отмечалось выше, матрица
, так как в противном случае, как отмечалось выше, матрица ![]() не имеет обратной.
не имеет обратной.
Проверим, что матрица
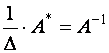 ,
,
т.е.
является обратной для матрицы ![]() .
.
Только для краткости записи
рассмотрим в качестве ![]() матрицу третьего
порядка. Тогда, с учетом свойств 9 и 10
определителей, получим
матрицу третьего
порядка. Тогда, с учетом свойств 9 и 10
определителей, получим

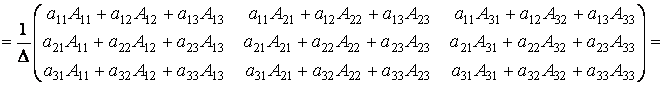
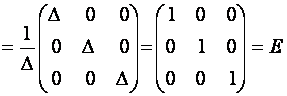 .
.
Совершенно аналогично проверяется, что
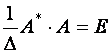 ,
,
и мы доказали, что обратную матрицу можно находить с помощью формулы
|
|
(6) |
Пример 6. Найдите
обратную матрицу ![]() для матрицы
для матрицы
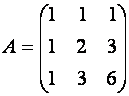 .
.
Решение.
Определитель матрицы
|
= |
Следовательно,
обратная матрица ![]() существует. Вычислим
алгебраические дополнения элементов
матрицы
существует. Вычислим
алгебраические дополнения элементов
матрицы ![]() :
:
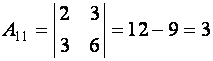 ,
, 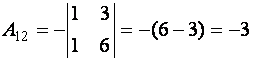 ,
,
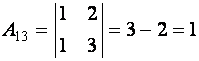 ,
, 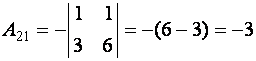 ,
,
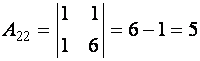 ,
, 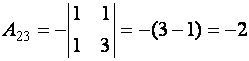 ,
,
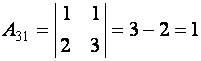 ,
, 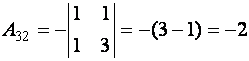 ,
,
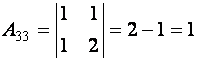 .
.
По формуле (6)
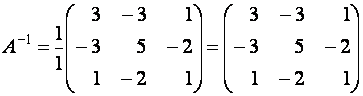 .
.
Проверим вычисления:
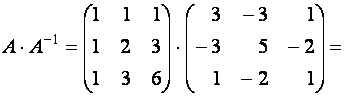
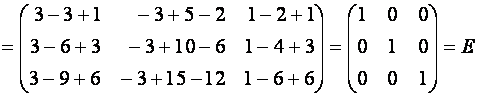 .
.
Ответ:
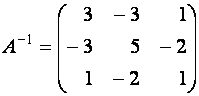 .
.
Пример 7. Найдите
обратную матрицу ![]() для матрицы
для матрицы
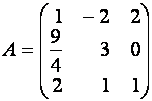 .
.
Решение.
Определитель матрицы ![]()
|
|
Матрица ![]() вырожденная и не имеет
обратной.
вырожденная и не имеет
обратной.
Ответ: матрица ![]() не имеет обратной.
не имеет обратной.


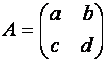
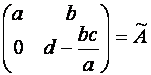
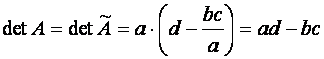 .
.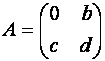
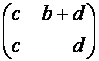
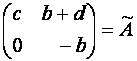
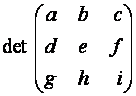
 .
.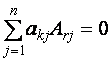 ,
,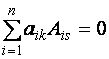 ,
,
 =
=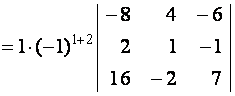
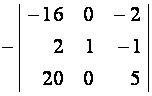 =
=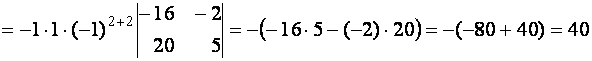 .
. =
=
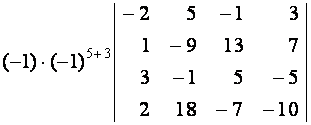 =
= 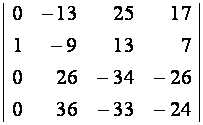
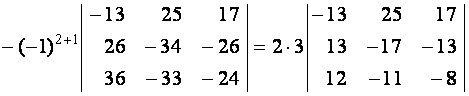

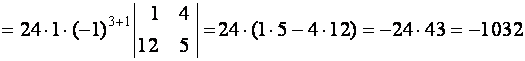 .
.
 .
.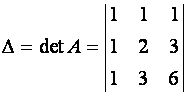 =
=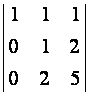 =
= 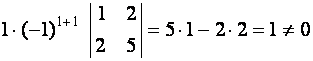 .
.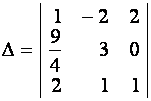
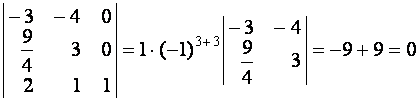 .
.