Опорные решения системы линейных уравнений
Применение
математических методов в экономике приводит к необходимости отыскания
неотрицательных решений системы линейных
уравнений, т.е. таких, в которых ![]() .
.
При
этом особое значение имеют неотрицательные базисные решения, которые принято
называть опорными решениями.
Таким образом, у опорных решений все базисные неизвестные должны иметь только неотрицательные значения.
Отсюда
естественным образом получается один из способов отыскания опорных решений
системы: из всех базисных решений выбрать одно, несколько или все (сколько
требуется по условию задачи) неотрицательные решения (конечно, если они
существуют в нужном количестве или вообще существуют).
Отсюда
же видно, что число опорных решений системы
может быть значительно меньше числа базисных решений, т.е. пытаться
предварительно отыскать все базисные решения – не слишком благодарная работа.
Еще раз отметим, что в базисном решении системы значения базисных неизвестных
равны свободным членам системы,
приведенной к единичному базису, и для того, чтобы базисное решение
оказалось опорным, необходимо и достаточно, чтобы эти свободные члены были
неотрицательными.
Поэтому
задачу отыскания опорных решений системы естественно начать с того, чтобы
сделать все ее свободные члены
неотрицательными (для этого каждое уравнение с отрицательным свободным членом
достаточно умножить на (-1)).
Далее можно воспользоваться тем же алгоритмом приведения
системы к единичному базису, что и при получении базисных решений, только его
следует дополнить специальным правилом
выбора ключевого элемента: ключевой столбец (допустим р-й)
выбирается так, чтобы он имел хотя бы один положительный элемент ![]() , и составляются отношения
, и составляются отношения ![]() свободных членов
свободных членов ![]() к соответствующим
положительным элементам ключевого столбца; то уравнение (пусть q-е), для
которого указанное отношение оказывается наименьшим, выбирается в качестве
ключевого (ключевой строки).
к соответствующим
положительным элементам ключевого столбца; то уравнение (пусть q-е), для
которого указанное отношение оказывается наименьшим, выбирается в качестве
ключевого (ключевой строки).
Таким
образом
|
|
(1) |
После
получения исходного (первого) опорного решения системы возникает вторая задача,
как последовательно перейти от него к следующему, тоже опорному решению.
Оказывается, для этого можно использовать алгоритм преобразования однократного
замещения, дополненный этим же правилом (1) выбора ключевого элемента.
Преобразования
системы с неотрицательными свободными членами к единичному базису, а также
преобразования однократного замещения (и те, и другие), при которых выбор
ключевого элемента производится по указанному правилу (1), принято называть симплексными преобразованиями.
Для
симплексных преобразований справедлива следующая теорема:
Ø
Если все свободные члены уравнений системы
неотрицательны, то после симплексных преобразований системы они останутся
неотрицательными.
Сформулированная
теорема подтверждает правило отыскания опорного решения методом Жордана-Гаусса, состоящее в соблюдении следующих условий:
1)
все свободные члены уравнений системы должны быть
неотрицательными; если есть хотя бы один отрицательный свободный член, то
соответствующее ему уравнение нужно умножить на (-1);
2)
в базис можно ввести только то неизвестное, у которого
есть хотя бы один положительный коэффициент;
3)
если при неизвестной, вводимой в базис, имеются
положительные коэффициенты в нескольких уравнениях, то неизвестная вводится в
базис в том уравнении, которому
соответствует наименьшее отношение свободных членов к этим положительным
коэффициентам.
Пример 1. Найдите опорное решение системы уравнений
 .
.
Решение.
Так
как во втором уравнении свободный член ![]() , умножим это уравнение на (-1). Заполним исходную
таблицу Гаусса.
, умножим это уравнение на (-1). Заполним исходную
таблицу Гаусса.
|
i |
Базис |
|
|
|
|
|
|
|
|
1 |
|
1 |
-2 |
1 |
2 |
-1 |
1 |
2 |
|
2 |
|
1 |
-1 |
2 |
-1 |
-1 |
2 |
2 |
|
3 |
|
2 |
0 |
1 |
-2 |
-1 |
2 |
2 |
Все
свободные члены положительные. При неизвестной ![]() есть
положительные коэффициенты, значит, можно ее ввести в базис. Поскольку
положительные коэффициенты при
есть
положительные коэффициенты, значит, можно ее ввести в базис. Поскольку
положительные коэффициенты при ![]() присутствуют
во всех трех уравнениях, следует найти (согласно
формуле (1)) минимальное отношение свободных членов к этим положительным
коэффициентам, т.е.
присутствуют
во всех трех уравнениях, следует найти (согласно
формуле (1)) минимальное отношение свободных членов к этим положительным
коэффициентам, т.е. 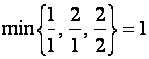 .
.
Это
минимальное отношение соответствует как первой, так и третьей строке,
следовательно, ![]() можно вводить в базис как в первом
уравнении, так и в третьем. Введем
можно вводить в базис как в первом
уравнении, так и в третьем. Введем ![]() в базис в
первом уравнении: ключевой элемент
в базис в
первом уравнении: ключевой элемент ![]() , ключевая строка первая, ключевой столбец первый.
, ключевая строка первая, ключевой столбец первый.
Составляем
таблицу Гаусса I итерации.
|
i |
Базис |
|
|
|
|
|
|
|
|
1 |
|
1 |
-2 |
1 |
2 |
-1 |
1 |
2 |
|
2 |
|
0 |
1 |
1 |
-3 |
0 |
1 |
0 |
|
3 |
|
0 |
4 |
-1 |
-6 |
1 |
0 |
-2 |
При
неизвестной ![]() есть положительные
коэффициенты в первом и во втором уравнениях, причем во втором уравнении нет
базисной переменной. Но
есть положительные
коэффициенты в первом и во втором уравнениях, причем во втором уравнении нет
базисной переменной. Но ![]() можно ввести в базис только в том случае, если минимальное
отношение свободных членов к положительным коэффициентам соответствует второму
уравнению.
можно ввести в базис только в том случае, если минимальное
отношение свободных членов к положительным коэффициентам соответствует второму
уравнению.
Находим 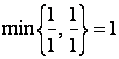 .
.
Отсюда
следует, что ![]() можно
ввести в базис во втором уравнении.
можно
ввести в базис во втором уравнении.
Составляем
таблицу Гаусса II итерации.
|
i |
Базис |
|
|
|
|
|
|
|
|
1 |
|
1 |
-3 |
0 |
5 |
-1 |
0 |
2 |
|
2 |
|
0 |
1 |
1 |
-3 |
0 |
1 |
0 |
|
3 |
|
0 |
5 |
0 |
-9 |
1 |
1 |
-2 |
При
неизвестной ![]() всего один
положительный коэффициент (в третьем уравнении), поэтому ее можно ввести в
базис в третьем уравнении.
всего один
положительный коэффициент (в третьем уравнении), поэтому ее можно ввести в
базис в третьем уравнении.
Составляем
таблицу Гаусса III итерации.
|
i |
Базис |
|
|
|
|
|
|
|
|
1 |
|
1 |
2 |
0 |
-4 |
0 |
1 |
0 |
|
2 |
|
0 |
1 |
1 |
-3 |
0 |
1 |
0 |
|
3 |
|
0 |
5 |
0 |
-9 |
1 |
1 |
-2 |
Итак,
система приведена к единичному базису. Выпишем общее решение системы
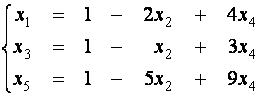
и опорное
решение ![]() .
.
Ответ : ![]() .
.
Пример 2. Найдите опорное решение системы уравнений
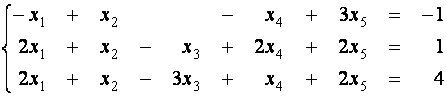 .
.
Решение.
Так
как ![]() , то в таблицу исходной системы запишем результат умножения
первого уравнения на (-1).
, то в таблицу исходной системы запишем результат умножения
первого уравнения на (-1).
|
i |
Базис |
|
|
|
|
|
|
|
|
1 |
|
1 |
-1 |
0 |
1 |
-3 |
1 |
-1 |
|
2 |
|
2 |
1 |
-1 |
2 |
2 |
1 |
7 |
|
3 |
|
2 |
1 |
-3 |
1 |
2 |
4 |
7 |
При
неизвестной ![]() есть два
положительных коэффициента и так как
есть два
положительных коэффициента и так как 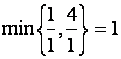 , то вводим
, то вводим ![]() в базис во
втором уравнении.
в базис во
втором уравнении.
В
таблице Гаусса I итерации
|
i |
Базис |
|
|
|
|
|
|
|
|
1 |
|
3 |
0 |
-1 |
3 |
-1 |
2 |
6 |
|
2 |
|
2 |
1 |
-1 |
2 |
2 |
1 |
7 |
|
3 |
|
0 |
0 |
-2 |
-1 |
0 |
3 |
0 |
неизвестную
![]() нельзя
ввести в базис, не выводя из него
нельзя
ввести в базис, не выводя из него ![]() , т.к.
, т.к. 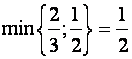 , что соответствует второму уравнению.
, что соответствует второму уравнению.
Точно так же нельзя ввести в базис неизвестную ![]() , не выводя из него
, не выводя из него ![]() , т.к.
, т.к. 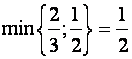 приходится на второе
уравнение. У неизвестной
приходится на второе
уравнение. У неизвестной ![]() единственный
положительный коэффициент также приходится на второе уравнение. У
неизвестной
единственный
положительный коэффициент также приходится на второе уравнение. У
неизвестной ![]() все коэффициенты отрицательные.
все коэффициенты отрицательные.
Поэтому
мы не можем получить опорное решение системы, вводя в базис первой неизвестную ![]() . Этот вывод можно было бы сделать быстрее, заметив, что в
третьей строке при положительном свободном члене
. Этот вывод можно было бы сделать быстрее, заметив, что в
третьей строке при положительном свободном члене ![]() нет ни одного положительного
коэффициента при неизвестных.
нет ни одного положительного
коэффициента при неизвестных.
Попытаемся
начать приведение системы к единичному базису с других неизвестных.
Для
неизвестной ![]() :
: 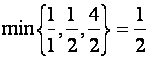 , поэтому вводим
, поэтому вводим ![]() в базис во втором
уравнении.
в базис во втором
уравнении.
При
этом исходная таблица имеет вид:
|
i |
Базис |
|
|
|
|
|
|
|
|
1 |
|
1 |
-1 |
0 |
1 |
-3 |
1 |
-1 |
|
2 |
|
2 |
1 |
-1 |
2 |
2 |
1 |
7 |
|
3 |
|
2 |
1 |
-3 |
1 |
2 |
4 |
7 |
В
третьей строке таблицы I итерации
|
i |
Базис |
|
|
|
|
|
|
|
|
1 |
|
0 |
- |
|
0 |
-4 |
|
- |
|
2 |
|
1 |
|
- |
1 |
1 |
|
|
|
3 |
|
0 |
0 |
-2 |
-1 |
0 |
3 |
0 |
опять нет
ни одного положительного коэффициента при неизвестных (при положительном
свободном члене). Поэтому мы не можем получить опорные решения, вводя в базис
первой неизвестную ![]() .
.
Для
неизвестной ![]() :
: 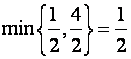 , поэтому вводим
, поэтому вводим ![]() в базис во втором
уравнении. При этом исходная таблица имеет вид:
в базис во втором
уравнении. При этом исходная таблица имеет вид:
|
i |
Базис |
|
|
|
|
|
|
|
|
1 |
|
1 |
-1 |
0 |
1 |
-3 |
1 |
-1 |
|
2 |
|
2 |
1 |
-1 |
2 |
2 |
1 |
7 |
|
3 |
|
2 |
1 |
-3 |
1 |
2 |
4 |
7 |
А
в третьей строке таблицы I итерации
та же картина:
|
i |
Базис |
|
|
|
|
|
|
|
|
1 |
|
4 |
|
- |
4 |
0 |
|
|
|
2 |
|
1 |
|
- |
1 |
1 |
|
|
|
3 |
|
0 |
0 |
-2 |
-1 |
0 |
3 |
0 |
Для
неизвестной ![]() :
: 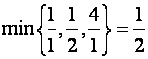 , поэтому вводим
, поэтому вводим ![]() в базис во втором
уравнении. При этом исходная таблица имеет вид:
в базис во втором
уравнении. При этом исходная таблица имеет вид:
|
i |
Базис |
|
|
|
|
|
|
|
|
1 |
|
1 |
-1 |
0 |
1 |
-3 |
1 |
-1 |
|
2 |
|
2 |
1 |
-1 |
2 |
2 |
1 |
7 |
|
3 |
|
2 |
1 |
-3 |
1 |
2 |
4 |
7 |
Таблица
I итерации выглядит так:
|
i |
Базис |
|
|
|
|
|
|
|
|
1 |
|
0 |
- |
|
0 |
-4 |
|
- |
|
2 |
|
1 |
|
- |
1 |
1 |
|
|
|
3 |
|
1 |
|
- |
0 |
1 |
|
|
Теперь
ни ![]() , ни
, ни ![]() , ни
, ни ![]() нельзя ввести в базис, не выводя из него
нельзя ввести в базис, не выводя из него ![]() . Остается
единственная возможность: ввести в базис
. Остается
единственная возможность: ввести в базис
![]() в первом уравнении. Получим
таблицу II итерации:
в первом уравнении. Получим
таблицу II итерации:
|
i |
Базис |
|
|
|
|
|
|
|
|
1 |
|
0 |
-3 |
1 |
0 |
-8 |
1 |
-9 |
|
2 |
|
1 |
-1 |
0 |
1 |
-3 |
1 |
-1 |
|
3 |
|
1 |
-7 |
0 |
0 |
-19 |
6 |
-19 |
Теперь в базис можно ввести лишь неизвестную ![]() , но только убрав из него
, но только убрав из него ![]() (так как
(так как 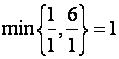 приходится на второе
уравнение).
приходится на второе
уравнение).
Мы
исчерпали все допустимые
возможности выбора первой базисной неизвестной
(и других) и не смогли получить опорного
решения. Следовательно, мы доказали, что данная система опорных решений не
имеет.
Ответ: система не имеет опорных решений.
Заметим,
что в нескольких случаях преобразования данной системы к единичному базису мы
приходили к одному и тому же уравнению ![]() , которое не может иметь неотрицательных решений. Легко
обнаружить, что это уравнение является следствием второго и третьего уравнений
исходной системы (оно получается вычитанием второго уравнения из третьего).
, которое не может иметь неотрицательных решений. Легко
обнаружить, что это уравнение является следствием второго и третьего уравнений
исходной системы (оно получается вычитанием второго уравнения из третьего).
Вспоминая, что при элементарных преобразованиях системы мы
получаем на каждом шаге систему, эквивалентную исходной, можем сделать полезный
практический вывод: если в процессе симплексных преобразований (а они также являются
элементарными) хотя бы в одном уравнении при положительном свободном члене нет
ни одного положительного коэффициента, то (так как оно не может иметь
неотрицательных решений) полученная система, а, следовательно, и исходная, не
имеют опорных решений.
Поэтому
в примере 2 поиски опорных решений можно было прекратить после получения
таблицы I итерации с
базисной неизвестной ![]() , которая уже содержала уравнение
, которая уже содержала уравнение ![]() (в третьей строке).
(в третьей строке).
Отметим,
что совместная система линейных уравнений может иметь хотя бы одно опорное
решение (пример 1), несколько опорных решений, не иметь опорных решений
(система примера 2; она совместная и имеет, что легко проверить, базисное решение
![]() , но не имеет опорных решений).
, но не имеет опорных решений).
Обратим
внимание на то обстоятельство, что некоторые неудобства в процесс отыскания
опорных решений могут внести свободные члены, равные нулю. Они могут
содержаться в исходной системе или могут
появиться в системе (даже если все начальные свободные члены были
положительны) в процессе симплексных преобразований, если при выборе ключевого
элемента минимальное отношение свободных членов к соответствующим коэффициентам
при неизвестной (формула ( 1)) одинаково хотя бы для двух уравнений. Так было при
решении примера 14: в I итерации
было получено ![]() , во II итерации
получилось
, во II итерации
получилось ![]() .
.
Неудобство нулевого свободного члена состоит в том, что он
может существенно ограничивать выбор
ключевого элемента (в первую очередь выбор ключевой строки), так как если в i-й строке с нулевым ![]() есть положительный коэффициент
при неизвестной, вводимой в базис, то она должна вводиться именно в этой, i-й строке, т.к. отношение,
равное 0, является минимальным (и единственным, если нет других нулевых
свободных членов).
есть положительный коэффициент
при неизвестной, вводимой в базис, то она должна вводиться именно в этой, i-й строке, т.к. отношение,
равное 0, является минимальным (и единственным, если нет других нулевых
свободных членов).
При
решении примера 1 этого неудобства не возникло, так как в таблице I итерации при ![]() коэффициент при
неизвестной
коэффициент при
неизвестной ![]() , вводимой в базис, оказался отрицательным
, вводимой в базис, оказался отрицательным ![]() , как и коэффициент
при неизвестной
, как и коэффициент
при неизвестной ![]() , вводимой в базис
в таблице II итерации при
, вводимой в базис
в таблице II итерации при ![]() . Но так бывает не всегда.
. Но так бывает не всегда.
Пример 3. Найдите опорное
решение системы
 .
.
Решение.
Заполним
исходную таблицу Гаусса.
|
i |
Базис |
|
|
|
|
|
|
|
|
1 |
|
-1 |
-2 |
-2 |
1 |
0 |
1 |
-3 |
|
2 |
|
2 |
1 |
2 |
-1 |
2 |
3 |
9 |
|
3 |
|
-1 |
-1 |
0 |
2 |
1 |
2 |
3 |
При
неизвестной ![]() есть два положительных
коэффициента и так как
есть два положительных
коэффициента и так как 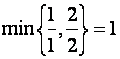 , то ввести
, то ввести ![]() в базис можно как в первом, так и в третьем уравнении.
Введем
в базис можно как в первом, так и в третьем уравнении.
Введем ![]() в базис в первом
уравнении.
в базис в первом
уравнении.
Получим
таблицу I итерации:
|
i |
Базис |
|
|
|
|
|
|
|
|
1 |
|
-1 |
-2 |
-2 |
1 |
0 |
1 |
-3 |
|
2 |
|
1 |
-1 |
0 |
0 |
2 |
4 |
6 |
|
3 |
|
1 |
3 |
4 |
0 |
1 |
0 |
9 |
Теперь
в базис можно вводить неизвестные ![]() ,
,![]() ,
, ![]() ,
, ![]() и только в третьем
уравнении (
и только в третьем
уравнении (![]() ). Введем в базис
). Введем в базис
![]() и заполним таблицу II итерации:
и заполним таблицу II итерации:
|
i |
Базис |
|
|
|
|
|
|
|
|
1 |
|
0 |
1 |
2 |
1 |
1 |
1 |
6 |
|
2 |
|
0 |
-4 |
-4 |
0 |
1 |
4 |
-3 |
|
3 |
|
1 |
3 |
4 |
0 |
1 |
0 |
9 |
Здесь
во втором (единственном неиспользованном уравнении) положительный коэффициент
только при ![]() , но
, но 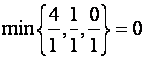 приходится на уже использованное
третье уравнение. Поэтому будем пробовать вводить в базис второй неизвестной
одну из неизвестных
приходится на уже использованное
третье уравнение. Поэтому будем пробовать вводить в базис второй неизвестной
одну из неизвестных![]() ,
, ![]() и
и ![]() (по очереди) и
заполнять новые таблицы I и II итерации.
(по очереди) и
заполнять новые таблицы I и II итерации.
Начнем
с неизвестной ![]() :
:
|
№ итерации |
i |
Базис |
|
|
|
|
|
|
|
|
I |
1 |
|
-1 |
-2 |
-2 |
1 |
0 |
1 |
-3 |
|
2 |
|
1 |
-1 |
0 |
0 |
2 |
4 |
6 |
|
|
3 |
|
1 |
3 |
4 |
0 |
1 |
0 |
9 |
|
|
II |
1 |
|
- |
0 |
|
1 |
|
1 |
3 |
|
2 |
|
|
0 |
|
0 |
|
4 |
9 |
|
|
3 |
|
|
1 |
|
0 |
|
0 |
3 |
Опять
возникла та же ситуация: вводить в базис можно
![]() ,
, ![]() и
и ![]() , но только в уже использованном
третьем уравнении.
, но только в уже использованном
третьем уравнении.
Результат
повторился бы, если бы вторую неизвестную вводили в базис ![]() или
или ![]() (читателю предоставляется
возможность убедиться в этом самостоятельно).
(читателю предоставляется
возможность убедиться в этом самостоятельно).
Возникает
предположение об отсутствии опорных решений у данной системы. И это
действительно лишь предположение: в отличие от примера 2 мы рассмотрели не все
допустимые возможности выбора базисных неизвестных (ведь первой неизвестной
могла быть выбрана не только ![]() , а и любая из остальных). Конечно, можно было бы продолжить
процесс симплексных преобразований исходной системы.
, а и любая из остальных). Конечно, можно было бы продолжить
процесс симплексных преобразований исходной системы.
Но
мы поступим иначе. Обратим внимание на третье уравнение системы, полученной
после первого симплексного преобразования:
![]() .
.
Все
его коэффициенты неотрицательны, а свободный член равен нулю. Поэтому, если система и имеет
хотя бы одно неотрицательное решение, то в нем обязательно должно быть ![]() и
и ![]() . В противном случае (если
хотя бы одна из перечисленных переменных отлична от нуля, т.е. положительна)
равенство невозможно (его левая часть будет положительной, а правая равна 0).
. В противном случае (если
хотя бы одна из перечисленных переменных отлична от нуля, т.е. положительна)
равенство невозможно (его левая часть будет положительной, а правая равна 0).
Остается
проверить, имеет ли система неотрицательные решения, у которых
![]() .
.
Подставляя
указанные значения неизвестных в исходную систему, получим систему трех
уравнений относительно неизвестной ![]() :
:
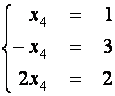
![]()
Она,
очевидно, несовместна. Следовательно, заданная система действительно не имеет
опорных решений.
Ответ: система не имеет опорных решений.
Пример 4. Найдите
опорное решение системы
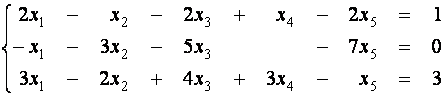 .
.
Решение.
Сразу замечаем, что во втором уравнении системы
свободный член равен нулю, а все
коэффициенты при переменных неположительны. Умножим
это уравнение на (-1) (при этом свободный член останется равным нулю, т.е.
неотрицательным): ![]() .
.
В
этом уравнении свободный член равен нулю, а все коэффициенты при переменных
неотрицательны. Отсюда следует, что если существует опорное решение данной
системы, то в нем ![]() . Подставляя в систему эти значения переменных, для неизвестного
. Подставляя в систему эти значения переменных, для неизвестного
![]() получаем систему двух
уравнений
получаем систему двух
уравнений
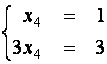
![]()
из которой находим ![]() .
.
Таким
образом единственное опорное решение данной системы ![]() .
.
Ответ: ![]() .
.
Примеры
3 и 4 показывают, что отыскание опорных решений системы, имеющей (или
приобретающей) хотя бы один нулевой свободный член требует повышенного внимания
и особой аккуратности. Поэтому (если, конечно, это представляется возможным) следует
такой ситуации избегать.
Заметим,
что, как и раньше, таблицы Гаусса исходной системы и всех последующих итераций
удобно записывать в виде одной большой таблицы, причем теперь (для симплексных
преобразований) мы дополним ее столбцом отношений свободных членов к нужным
положительным элементам столбцов с переменными (т.е. к положительным элементам
будущих ключевых столбцов).
Пример 5. Найдите
опорное решение системы
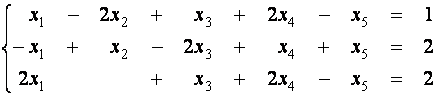 .
.
Решение.
Таблица 1
|
№ итерации |
i |
Базис |
|
|
|
|
|
|
|
|
|
Исходная система |
1 |
|
1 |
-2 |
1 |
2 |
-1 |
1 |
2 |
|
|
2 |
|
-1 |
1 |
-2 |
1 |
1 |
2 |
2 |
|
|
|
3 |
|
2 |
0 |
1 |
2 |
-1 |
2 |
6 |
|
|
|
I |
1 |
|
0 |
-1 |
-1 |
3 |
0 |
3 |
4 |
|
|
2 |
|
-1 |
1 |
-2 |
1 |
1 |
2 |
2 |
|
|
|
3 |
|
1 |
1 |
-1 |
3 |
0 |
4 |
8 |
|
|
|
II |
1 |
|
0 |
-1 |
-1 |
3 |
0 |
3 |
4 |
1 |
|
2 |
|
0 |
2 |
-3 |
4 |
1 |
6 |
10 |
|
|
|
3 |
|
1 |
1 |
-1 |
3 |
0 |
4 |
8 |
|
|
|
III |
1 |
|
0 |
- |
- |
1 |
0 |
1 |
|
|
|
2 |
|
0 |
|
- |
0 |
1 |
2 |
|
|
|
|
3 |
|
1 |
2 |
0 |
0 |
0 |
1 |
4 |
|
В результате симплексных преобразований (в таблицах Гаусса) система приведена к единичному базису. Общее решение системы имеет вид:
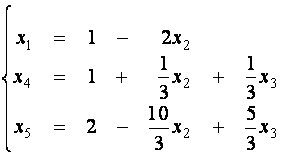 ,
, ![]() .
.
Ответ: ![]() .
.
Как
уже отмечалось, с помощью симплексных преобразований можно найти не только
одно, а
и несколько опорных решений (или даже все) данной системы линейных
уравнений.
Для
этого к системе, приведенной к единичному базису и определяющей тем самым
какое-то одно (исходное) опорное решение, следует применить симплексное
преобразование однократного замещения. В результате получится новое опорное
решение.
Осуществить это симплексное преобразование можно
лишь в том случае, если в
соответствующей системе есть хотя бы
один положительный коэффициент при какой-либо свободной переменной. Если же все
коэффициенты при всех свободных переменных отрицательны или равны нулю, то
перейти к другому опорному решению
нельзя.
Так,
в таблице III итерации
примера 5 (определяющей опорное решение) у свободной переменной ![]() нет положительных
коэффициентов, а у свободной переменной
нет положительных
коэффициентов, а у свободной переменной ![]() - есть,
причем два. Так как
- есть,
причем два. Так как 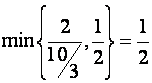 , то переменную
, то переменную ![]() можно ввести
в базис в третьем уравнении (вместо переменной
можно ввести
в базис в третьем уравнении (вместо переменной ![]() ).
).
Перепишем
вновь таблицу III итерации и
заполним таблицу IV итерации:
|
III ' |
1 |
|
0 |
- |
- |
1 |
0 |
1 |
|
|
|
2 |
|
0 |
|
- |
0 |
1 |
2 |
|
|
|
|
3 |
|
1 |
2 |
0 |
0 |
0 |
1 |
4 |
|
|
|
IV |
1 |
|
|
0 |
- |
1 |
0 |
|
2 |
|
|
2 |
|
- |
0 |
- |
0 |
1 |
|
-2 |
|
|
|
3 |
|
|
1 |
0 |
0 |
0 |
|
2 |
|
Из
таблицы IV итерации
находим 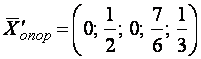 .
.
В
таблице IV итерации у свободной переменной ![]() нет положительных коэффициентов,
а у переменной
нет положительных коэффициентов,
а у переменной ![]() - есть (два). И так
как
- есть (два). И так
как 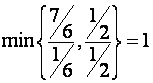 , то
, то ![]() можно
ввести в базис вместо
можно
ввести в базис вместо ![]() и получить
базисные переменные
и получить
базисные переменные ![]() , что уже было в первом опорном решении.
, что уже было в первом опорном решении.
Следовательно,
новых опорных решений получить нельзя и система примера 18 имеет только два
опорных решения:
![]() и
и 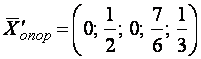 .
.
Пример 6. Найдите
все опорные решения системы
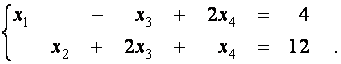
Решение.
Таблица 2
|
№ итерации |
i |
Базис |
|
|
|
|
|
|
|
Опорные
решения |
|
Исходная система |
1 |
|
1 |
0 |
-1 |
2 |
4 |
6 |
|
|
|
2 |
|
0 |
1 |
2 |
1 |
12 |
16 |
|
||
|
I |
1 |
|
1 |
|
0 |
|
10 |
14 |
4 |
|
|
2 |
|
0 |
|
1 |
|
6 |
8 |
12 |
||
|
II |
1 |
|
|
|
0 |
1 |
4 |
|
20 |
|
|
2 |
|
- |
|
1 |
0 |
4 |
|
10 |
||
|
III |
1 |
|
|
0 |
- |
1 |
2 |
3 |
|
|
|
2 |
|
- |
1 |
|
0 |
10 |
13 |
|
В
последнем столбце таблицы 2 указаны четыре опорных решения данной системы,
соответствующие таким парам базисных
переменных: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ; при этом буква
; при этом буква
![]() означает номер
переменной, вводимой в базис на следующей итерации, а буква
означает номер
переменной, вводимой в базис на следующей итерации, а буква ![]() - номер уравнения, в котором это происходит.
- номер уравнения, в котором это происходит.
Заметим,
что базисных решений эта система имеет 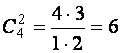 . Среди четырех полученных опорных решений отсутствуют
решения с базисными переменными
. Среди четырех полученных опорных решений отсутствуют
решения с базисными переменными ![]() и
и ![]() .
.
Анализ
таблицы 2 показывает, что эти пары переменных нельзя ввести в базис при
симплексных преобразованиях системы. При этом III итерация дала последнее
опорное решение ![]() . Если теперь выбрать
. Если теперь выбрать ![]() , то получим
, то получим ![]() и придем к базису, состоящему из векторов
и придем к базису, состоящему из векторов ![]() , а такой базис уже фигурировал в исходной системе. Выбирая
, а такой базис уже фигурировал в исходной системе. Выбирая ![]() , найдем
, найдем ![]() и получим базис, участвовавший
во II итерации.
и получим базис, участвовавший
во II итерации.
Ответ: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Пример 7. Найдите
все опорные решения системы
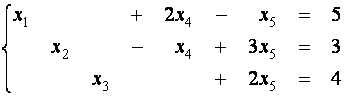 .
.
Решение.
Таблица 3
|
№ итерации |
i |
Базис |
|
|
|
|
|
|
|
|
Опорные
решения |
|
Исходная система |
1 |
|
1 |
0 |
0 |
2 |
-1 |
5 |
7 |
|
|
|
2 |
|
0 |
1 |
0 |
-1 |
3 |
3 |
6 |
1 |
||
|
3 |
|
0 |
0 |
1 |
0 |
2 |
4 |
7 |
2 |
|
I |
1 |
|
1 |
|
0 |
|
0 |
6 |
9 |
|
|
|
2 |
|
0 |
|
0 |
- |
1 |
1 |
2 |
|
||
|
3 |
|
0 |
- |
1 |
|
0 |
2 |
3 |
3 |
||
|
II |
1 |
|
1 |
2 |
- |
0 |
0 |
1 |
|
|
|
|
2 |
|
0 |
0 |
|
0 |
1 |
2 |
|
|
||
|
3 |
|
0 |
-1 |
|
1 |
0 |
3 |
|
|
||
|
III |
1 |
|
|
1 |
- |
0 |
0 |
|
|
|
|
|
2 |
|
0 |
0 |
|
0 |
1 |
2 |
|
7 |
||
|
3 |
|
|
0 |
|
1 |
0 |
|
|
21 |
||
|
IV |
1 |
|
|
1 |
0 |
0 |
|
|
|
|
|
|
2 |
|
0 |
0 |
1 |
0 |
2 |
4 |
7 |
|
||
|
3 |
|
|
0 |
0 |
1 |
- |
|
|
|
После
проведения IV итерации
получено последнее (пятое) опорное решение. В самом деле, если выбрать ![]() , то получим
, то получим ![]() и базис из векторов
и базис из векторов ![]() , но к нему уже была приведена исходная система. Если же
взять
, но к нему уже была приведена исходная система. Если же
взять ![]() , то получим
, то получим ![]() и базис, участвовавший
в III итерации.
и базис, участвовавший
в III итерации.
Ответ: ![]() ,
, ![]() ,
, ![]() ,
,
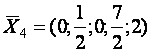 ,
, 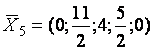 .
.
Пример 8. Найдите общее и опорное решение системы. Перейдите от одного опорного решения к другому.
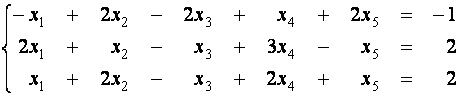 .
.
Решение.
Таблица 4
|
№ итерации |
i |
Базис |
|
|
|
|
|
|
|
|
Опорные
решения |
|
Исходная система |
1 |
|
1 |
-2 |
2 |
-1 |
-2 |
1 |
-1 |
1 |
|
|
2 |
|
2 |
1 |
-1 |
3 |
-1 |
2 |
6 |
1 |
||
|
3 |
|
1 |
2 |
-1 |
2 |
1 |
2 |
7 |
2 |
||
|
I |
1 |
|
1 |
-2 |
2 |
-1 |
-2 |
1 |
-1 |
|
|
|
2 |
|
0 |
5 |
-5 |
5 |
3 |
0 |
8 |
0 |
||
|
3 |
|
0 |
4 |
-3 |
3 |
3 |
1 |
8 |
|
||
|
II |
1 |
|
1 |
0 |
0 |
1 |
- |
1 |
|
|
|
|
2 |
|
0 |
1 |
-1 |
1 |
|
0 |
|
|
||
|
3 |
|
0 |
0 |
1 |
-1 |
|
1 |
|
|
||
|
III |
1 |
|
1 |
0 |
0 |
1 |
- |
1 |
|
|
|
|
2 |
|
0 |
1 |
0 |
0 |
|
1 |
|
|
||
|
3 |
|
0 |
0 |
1 |
-1 |
|
1 |
|
|
||
|
IV |
1 |
|
1 |
0 |
0 |
1 |
- |
1 |
|
|
|
|
2 |
|
0 |
1 |
0 |
0 |
|
1 |
|
|
||
|
3 |
|
1 |
0 |
1 |
0 |
- |
2 |
|
|
Из
таблицы III итерации
выписываем общее решение (которому соответствует первое опорное решение ![]() ):
):
 .
.
Можно было бы выписать общее решение из таблицы IV итерации (которому соответствует второе опорное решение
![]() ):
):
 .
.
Ответ: общее решение системы

![]()
опорные
решения ![]() ,
, ![]() .
.
Пример 9. Найдите
общее и опорное решение системы. Перейдите от одного опорного решения к другому:
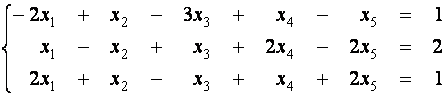 .
.
Решение.
Таблица 5
|
№ итерации |
i |
Базис |
|
|
|
|
|
|
|
|
Опорные
решения |
|
Исходная система |
1 |
|
-2 |
1 |
-3 |
1 |
-1 |
1 |
-3 |
1 |
|
|
2 |
|
1 |
-1 |
1 |
2 |
-2 |
2 |
3 |
1 |
||
|
3 |
|
2 |
1 |
-1 |
1 |
2 |
1 |
6 |
1 |
||
|
I |
1 |
|
-2 |
1 |
-3 |
1 |
-1 |
1 |
-3 |
|
|
|
2 |
|
5 |
-3 |
7 |
0 |
0 |
0 |
9 |
0 |
||
|
3 |
|
4 |
0 |
2 |
0 |
3 |
0 |
9 |
0 |
|
II |
1 |
|
4 |
1 |
0 |
1 |
|
1 |
|
|
Умножим 2е
уравнение на (- |
|
2 |
|
-9 |
-3 |
0 |
0 |
- |
0 |
- |
|
||
|
3 |
|
2 |
0 |
1 |
0 |
|
0 |
|
|
||
|
II' |
1 |
|
4 |
1 |
0 |
1 |
|
1 |
|
1 |
|
|
2 |
|
3 |
1 |
0 |
0 |
|
0 |
|
0 |
||
|
3 |
|
2 |
0 |
1 |
0 |
|
0 |
|
|
||
|
III |
1 |
|
1 |
0 |
0 |
1 |
0 |
1 |
3 |
|
|
|
2 |
|
3 |
1 |
0 |
0 |
|
0 |
|
|
||
|
3 |
|
2 |
0 |
1 |
0 |
|
0 |
|
|
Общее
решение имеет вид

![]()
В
опорном решении ![]() равными нулю оказались
не только свободные переменные
равными нулю оказались
не только свободные переменные ![]() и
и ![]() , но и две базисные -
, но и две базисные - ![]() и
и ![]() . Этот результат мы могли получить и раньше, обратив
внимание, что в третьей строке I итерации
симплексной таблицы 5 все коэффициенты оказались неотрицательными при нулевом
свободном члене. Из уравнения
. Этот результат мы могли получить и раньше, обратив
внимание, что в третьей строке I итерации
симплексной таблицы 5 все коэффициенты оказались неотрицательными при нулевом
свободном члене. Из уравнения ![]() следует:
следует: ![]() . Теперь система
относительно остальных неизвестных
. Теперь система
относительно остальных неизвестных ![]() и
и ![]() записывается в виде
записывается в виде
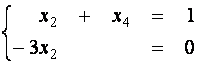
![]()
откуда ![]() и
и ![]() .
.
Поэтому
единственное неотрицательное решение
исходной системы есть ![]() .
.
Ответ: общее решение системы
 ,
,
единственное
опорное решение ![]() .
.
Пример 10. Найдите
опорное решение системы и перейдите от одного решения к другому. Выпишите общее
решение системы.
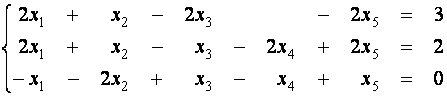 .
.
Решение.
Таблица 6
|
№ итерации |
i |
Базис |
|
|
|
|
|
|
|
|
|
Исходная система |
1 |
|
2 |
1 |
-2 |
0 |
-2 |
3 |
2 |
|
|
2 |
|
2 |
1 |
-1 |
-2 |
2 |
2 |
4 |
1 |
|
|
3 |
|
-1 |
-2 |
1 |
-1 |
1 |
0 |
-2 |
|
|
|
I |
1 |
|
0 |
0 |
-1 |
2 |
-4 |
1 |
-2 |
|
|
2 |
|
1 |
|
- |
-1 |
1 |
1 |
2 |
1 |
|
|
3 |
|
0 |
- |
|
-2 |
2 |
1 |
0 |
|
|
|
II |
1 |
|
0 |
-3 |
0 |
-2 |
0 |
3 |
-2 |
|
|
2 |
|
1 |
|
- |
0 |
0 |
|
2 |
|
|
|
3 |
|
0 |
- |
|
-1 |
1 |
|
0 |
|
Замечаем,
что в первой строке таблицы II итерации
все коэффициенты не положительны при
положительном свободном члене. Соответствующее уравнение имеет вид ![]() .
.
Это
уравнение (а вместе с ним и вся полученная после второго симплексного преобразования
система уравнений) не имеет неотрицательных решений.
Следовательно,
исходная система опорных решений не имеет.
Теперь,
отказавшись от требования неотрицательности переменных, найдем общее решение системы,
введя в III итерации в
число базисных переменных ![]() в первом уравнении (
в первом уравнении (![]() ).
).
|
№ итерации |
i |
Базис |
|
|
|
|
|
|
|
|
III |
1 |
|
0 |
1 |
0 |
|
0 |
-1 |
|
|
2 |
|
1 |
0 |
- |
- |
0 |
|
|
|
|
3 |
|
0 |
0 |
|
- |
1 |
- |
|
Ответ: общее решение системы имеет вид:
 ,
,
опорных решений нет.
 .
.