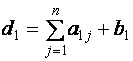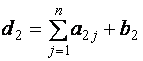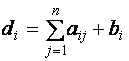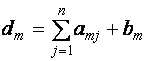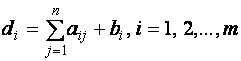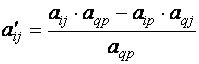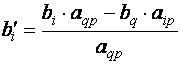Таблицы Гаусса
Решение
систем линейных уравнений методом Жордана-Гаусса
технически удобно проводить с помощью так называемых таблиц Гаусса, которые имеют следующий вид:
|
№
уравнения i |
Базис |
|
|
… |
|
… |
|
|
Контрольный
столбец |
|
1 |
|
|
|
… |
|
… |
|
|
|
|
2 |
|
|
|
… |
|
… |
|
|
|
|
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
|
|
… |
|
… |
|
|
|
|
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
|
|
… |
|
… |
|
|
|
В
первую (исходную) таблицу записывается расширенная матрица системы
и вычисляются элементы контрольного столбца по формуле
|
|
(1) |
Далее
приступают к выполнению первой итерации согласно следующему алгоритму
(правилу):
1)
Выбирают переменную, которую вводят в базис;
соответствующий столбец в таблице выделяется и называется ключевым (пусть это будет р-ый столбец).
2)
Выбирается строка, из которой вводят в базис
переменную ![]() ; эту строку называют ключевой
и ее также выделяют (пусть это будет
; эту строку называют ключевой
и ее также выделяют (пусть это будет ![]() -ая строка). Элемент
-ая строка). Элемент ![]() , стоящий на пересечении ключевых
строки и столбца, называется ключевым
элементом. Он должен быть отличен от нуля (
, стоящий на пересечении ключевых
строки и столбца, называется ключевым
элементом. Он должен быть отличен от нуля (![]() ¹0).
¹0).
3)
Составляется следующая таблица, которую заполняют так:
а) Элементы ключевой строки
делят на ключевой элемент
 ;
;
б) Суммируются все новые
элементы ключевой строки (без ![]() ), и результат сравнивается с
найденным элементом
), и результат сравнивается с
найденным элементом ![]() . Если расхождений нет, то переходят к пункту в). Если
обнаружено расхождение, то производится пересчет элементов
. Если расхождений нет, то переходят к пункту в). Если
обнаружено расхождение, то производится пересчет элементов ![]() и
и ![]() для выявления ошибки;
для выявления ошибки;
в) Заполняют базисный столбец (он единичный);
г) Остальные элементы, в том
числе и свободные члены, и элементы контрольного столбца, находят по правилу прямоугольника. При этом расчет
производится по строкам;
д) После
вычисления элементов каждой строки производится их суммирование и сравнение
результата с элементом контрольного столбца как в пункте в).
На
этом заканчивается выполнение одной итерации, после чего весь расчет
повторяется с пункта 1.
Правилом прямоугольника называют
формулу
|
|
(2) |
Оно
заключается в следующем: чтобы найти новый элемент ![]() , следует построить прямоугольник, у которого две
противоположные вершины занимают старый элемент
, следует построить прямоугольник, у которого две
противоположные вершины занимают старый элемент ![]() и ключевой элемент
и ключевой элемент ![]() , а две другие вершины занимают элементы
, а две другие вершины занимают элементы ![]() из ключевой строки и
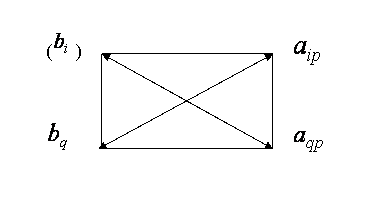
из ключевой строки и ![]() из ключевого столбца:
из ключевого столбца:
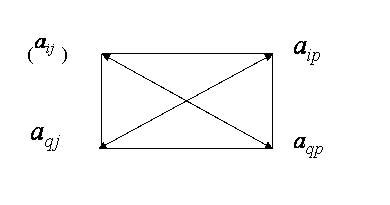
т.е.
искомый элемент равен разности произведений элементов, стоящих в
противоположных вершинах этого прямоугольника (причем первым берется
произведение, содержащее ключевой элемент), деленной на ключевой элемент.
При
этом свободные члены вычисляются по формуле
|
|
(3) |
а элементы
контрольного столбца вычисляются по формуле
|
|
(4) |
Замечание 1.
Целесообразно, если это возможно, выбирать
ключевой элемент равным 1, так как при этом упрощаются вычисления.
Замечание 2. Если в
ключевой строке (столбце) находится нулевой элемент ![]() = 0 (или
= 0 (или ![]() = 0), то, как следует
из формулы (2), соответствующий ему
= 0), то, как следует
из формулы (2), соответствующий ему ![]() -ый столбец (
-ый столбец (![]() -ая строка) остается на данном
этапе преобразований неизменным.
-ая строка) остается на данном
этапе преобразований неизменным.
Проиллюстрируем изложенную методику расчета на примерах.
Пример 1. Решите с помощью таблиц Гаусса следующую систему уравнений
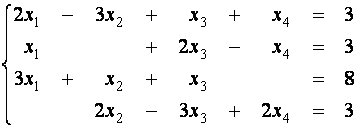 .
.
Решение.
Таблица 1 (исходная)
|
i |
Базис |
|
|
|
|
|
|
|
1 |
|
2 |
-3 |
1 |
1 |
3 |
4 |
|
2 |
|
1 |
0 |
2 |
-1 |
3 |
5 |
|
3 |
|
3 |
1 |
1 |
0 |
8 |
13 |
|
4 |
|
0 |
2 |
-3 |
2 |
3 |
4 |
В
исходной таблице выбрали в качестве ключевого элемента ![]() = 1 (т.е. q
= 2, p = 1), ключевая строка – вторая, ключевой столбец –
первый, т.е. ввели в базис
= 1 (т.е. q
= 2, p = 1), ключевая строка – вторая, ключевой столбец –
первый, т.е. ввели в базис ![]() во
втором уравнении.
во
втором уравнении.
Таблица 2 (I итерация)
|
i |
Базис |
|
|
|
|
|
|
|
1 |
|
0 |
-3 |
-3 |
3 |
-3 |
-6 |
|
2 |
|
1 |
0 |
2 |
-1 |
3 |
5 |
|
3 |
|
0 |
1 |
-5 |
3 |
-1 |
-2 |
|
4 |
|
0 |
2 |
-3 |
2 |
3 |
4 |
Вторую
таблицу начинаем заполнять с элементов ключевой строки (в данном случае она
переписывается без изменения, так как ![]() = 1).
= 1).
В
первом столбце записываются нули (кроме ![]() = 1). Вычисление остальных элементов проводим по правилу
прямоугольника.
= 1). Вычисление остальных элементов проводим по правилу
прямоугольника.
Так,
например, для элемента ![]() = 1 исходной таблицы получаем в новой таблице
= 1 исходной таблицы получаем в новой таблице ![]() , аналогично
, аналогично ![]() ,
, ![]() ,
, ![]() и т.д.
и т.д.
Заметим,
что элемент ключевой строки ![]() = 0 и элемент ключевого столбца
= 0 и элемент ключевого столбца ![]() = 0, поэтому в новой таблице второй столбец и четвертая
строка остались без изменения.
= 0, поэтому в новой таблице второй столбец и четвертая
строка остались без изменения.
После
окончания первой итерации получаем один единичный столбец ![]() . Для проведения II итерации выбираем в качестве ключевого элемента
. Для проведения II итерации выбираем в качестве ключевого элемента ![]() = 1, т.е. вводим в
базис
= 1, т.е. вводим в
базис ![]() в третьем
уравнении.
в третьем
уравнении.
Далее
расчет выполняется аналогично предыдущему. Так, например,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Таблица 3 (II итерация)
|
i |
Базис |
|
|
|
|
|
|
|
1 |
|
0 |
0 |
-18 |
12 |
-6 |
-12 |
|
2 |
|
1 |
0 |
2 |
-1 |
3 |
5 |
|
3 |
|
0 |
1 |
-5 |
3 |
-1 |
-2 |
|
4 |
|
0 |
0 |
7 |
-4 |
5 |
8 |
После
окончания II итерации
добавляется еще один единичный столбец ![]() .
.
III итерацию начинаем с выбора
ключевого элемента ![]() =12, т.е. вводим в базис
=12, т.е. вводим в базис ![]() в первом уравнении.
Ключевая строка будет выглядеть так (после деления всех ее элементов на
в первом уравнении.
Ключевая строка будет выглядеть так (после деления всех ее элементов на ![]() = 12) :
= 12) :
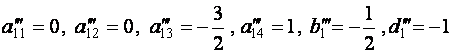 .
.
Далее
используем правило прямоугольника.
Например,
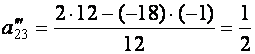 ,
, 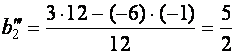 ,
,
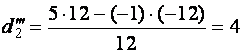 .
.
Таблица 4 (III итерация)
|
i |
Базис |
|
|
|
|
|
|
|
1 |
|
0 |
0 |
- |
1 |
- |
-1 |
|
2 |
|
1 |
0 |
|
0 |
|
4 |
|
3 |
|
0 |
1 |
- |
0 |
|
1 |
|
4 |
|
0 |
0 |
1 |
0 |
3 |
4 |
После
окончания III итерации
добавился еще один единичный столбец ![]() .
.
Наконец,
IV итерацию начинаем с выбора
ключевого элемента ![]() , т.е. вводим в базис
, т.е. вводим в базис ![]() в четвертом уравнении.
в четвертом уравнении.
Таблица 5 (IV итерация)
|
i |
Базис |
|
|
|
|
|
|
|
1 |
|
0 |
0 |
0 |
1 |
4 |
5 |
|
2 |
|
1 |
0 |
0 |
0 |
1 |
2 |
|
3 |
|
0 |
1 |
0 |
0 |
2 |
3 |
|
4 |
|
0 |
0 |
1 |
0 |
3 |
4 |
После
проведения IV
итерации добавился еще один единичный
вектор ![]() , и мы получили систему, приведенную к единичному базису
, и мы получили систему, приведенную к единичному базису ![]() .
.
Так
как число базисных неизвестных (![]() = 4) оказалось равным числу всех неизвестных (
= 4) оказалось равным числу всех неизвестных (![]() = 4), то система определенная.
= 4), то система определенная.
Ее
единственное решение находим из последней таблицы (Таблица 5):
![]() .
.
Ответ: ![]() .
.
Заметим, что на практике все 5 таблиц Гаусса, использованных, чтобы найти решение для системы примера 1, можно объединить в одну большую таблицу, записывая их подряд одну под другой, а номер соответствующей итерации указывая слева от таблицы.
Мы
воспользуемся этим замечанием в последующих примерах.
Пример 2. Решите в таблице Гаусса систему уравнений
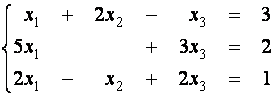 .
.
Решение.
Таблица 6
|
№ итерации |
i |
Базис |
|
|
|
|
|
|
Исходная система |
1 |
|
1 |
2 |
-1 |
3 |
5 |
|
2 |
|
5 |
0 |
3 |
2 |
10 |
|
|
3 |
|
2 |
-1 |
2 |
1 |
4 |
|
|
I |
1 |
|
1 |
2 |
-1 |
3 |
5 |
|
2 |
|
0 |
-10 |
8 |
-13 |
-15 |
|
|
3 |
|
0 |
-5 |
4 |
-5 |
-6 |
|
II |
1 |
|
1 |
0 |
|
1 |
|
|
2 |
|
0 |
1 |
- |
|
|
|
|
3 |
|
0 |
0 |
0 |
|
|
Полученная
после II итерации система содержит одно
противоречивое уравнение (третье):
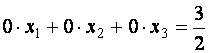 ,
,
откуда
следует вывод о несовместности исходной системы.
Ответ: система несовместна.
Пример 3. Найдите общее и базисное решение системы
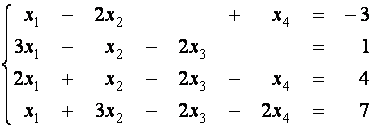 .
.
Решение.
Таблица 7
|
№ итерации |
i |
Базис |
|
|
|
|
|
|
|
Исходная система |
1 |
|
1 |
-2 |
0 |
1 |
-3 |
-3 |
|
2 |
|
3 |
-1 |
-2 |
0 |
1 |
1 |
|
|
3 |
|
2 |
1 |
-2 |
-1 |
4 |
4 |
|
|
4 |
|
1 |
3 |
-2 |
-2 |
7 |
7 |
|
I |
1 |
|
1 |
-2 |
0 |
1 |
-3 |
-3 |
|
2 |
|
0 |
5 |
-2 |
-3 |
10 |
10 |
|
|
3 |
|
0 |
5 |
-2 |
-3 |
10 |
10 |
|
|
4 |
|
0 |
5 |
-2 |
-3 |
10 |
10 |
|
|
II |
1 |
|
1 |
0 |
- |
- |
1 |
1 |
|
2 |
|
0 |
1 |
- |
- |
2 |
2 |
|
|
3 |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|
4 |
|
0 |
0 |
0 |
0 |
0 |
0 |
После
первой итерации получили три совпадающие строки, откуда следует, что два
уравнения из последних трех "лишние". На следующей итерации эти
строки превратились в нулевые и могут быть отброшены.
В
результате получили два уравнения (ранг системы ![]() = 2), которые разрешены относительно неизвестных
= 2), которые разрешены относительно неизвестных ![]() и
и ![]() (базисные
неизвестные):
(базисные
неизвестные):
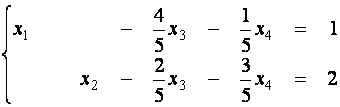 .
.
Таким
образом, система оказалась совместной и неопределенной.
Ее
общее решение
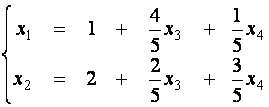
может быть
получено и непосредственно из таблицы второй итерации. Обратим лишь внимание на
тот факт, что коэффициенты при свободных неизвестных в общем решении отличаются
знаком от содержащихся в таблице.
Полагая
свободные неизвестные ![]() = 0,
= 0, ![]() = 0, находим
= 0, находим ![]() = 1,
= 1, ![]() = 2 и базисное решение
= 2 и базисное решение ![]() .
.
Ответ: общее решение системы
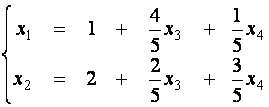 ,
, ![]() .
.
Заметим,
что если система приведена к единичному базису, то можно сразу без всяких
вычислений найти соответствующее ей базисное решение. Для
этого достаточно положить свободные неизвестные равными нулю, а базисные -
соответствующим свободным членам.
Будем
называть это базисное решение соответствующим
приведенной системе.
Однако
исходная система может иметь не одно базисное решение. Чтобы найти их, можно
было бы в исходной (или приведенной) системе положить равными нулю другие
неизвестные (в том же количестве), приняв их тем самым за
свободные, и определить значения базисных неизвестных.
Но этот путь связан с относительно громоздкими расчетами.
Более
целесообразно систему, приведенную к одному единичному базису, преобразовать в
систему, приведенную к другому единичному базису, после чего немедленно
определяется соответствующее этой
приведенной системе новое базисное решение.
Удобнее
всего с этой целью применить преобразование
однократного замещения, когда в уже приведенной системе ровно одна базисная
переменная заменяется на новую.
При
проведении расчетов в таблицах Гаусса это преобразование сводится после отыскания одного (первого) базисного решения
к выполнению еще одной итерации метода Жордана-Гаусса
для получения каждого нового базисного решения.
Пример 4. Найдите все базисные решения системы
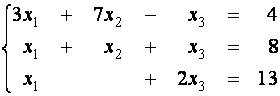 .
.
Решение.
Таблица 8
|
№ итерации |
i |
Базис |
|
|
|
|
|
Базисноерешение |
|
Исходная система |
1 |
|
3 |
7 |
-1 |
4 |
13 |
|
|
2 |
|
1 |
1 |
1 |
8 |
11 |
|
|
|
3 |
|
1 |
0 |
2 |
13 |
16 |
|
|
|
I |
1 |
|
0 |
4 |
-4 |
-20 |
-20 |
|
|
2 |
|
1 |
1 |
1 |
8 |
11 |
|
|
|
3 |
|
0 |
-1 |
1 |
5 |
5 |
|
|
|
II |
1 |
|
0 |
0 |
0 |
0 |
0 |
|
|
2 |
|
1 |
2 |
0 |
3 |
6 |
||
|
3 |
|
0 |
-1 |
1 |
5 |
5 |
|
III |
2 |
|
|
1 |
0 |
|
3 |
|
|
3 |
|
|
0 |
1 |
|
8 |
||
|
IV |
2 |
|
0 |
1 |
-1 |
-5 |
-5 |
|
|
3 |
|
1 |
0 |
2 |
13 |
16 |
Ответ: базисные решения ![]() ,
, ![]() ,
, ![]() .
.
Число базисных решений оказалось максимально возможным – три.
Так как ранг системы ![]() = 2, количество неизвестных
= 2, количество неизвестных ![]() = 3, то
= 3, то 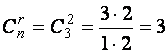 .
.
Но так бывает не всегда.
Пример 5. Найдите все базисные решения следующей системы уравнений
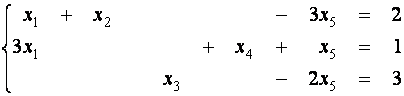 .
.
Решение.
Заметим,
что исходная система уже приведена к единичному базису ![]() и
и ![]() с базисными
неизвестными
с базисными
неизвестными ![]() и свободными
и свободными ![]() и
и ![]() . Соответствующее базисное решение
. Соответствующее базисное решение ![]() .
.
Отыскание
других базисных решений будем проводить методом последовательных преобразований
однократного замещения. При этом нужно лишь следить за тем, чтобы в процессе
преобразований не повторился ранее встречавшийся базис. Для этого следует
систематизировать расчеты. Прежде всего определим, сколько всего базисных решений может иметь данная система. Так как
ранг системы ![]() = 3, а число неизвестных
= 3, а число неизвестных ![]() = 5, то максимально возможное число различных групп базисных неизвестных будет равно
= 5, то максимально возможное число различных групп базисных неизвестных будет равно 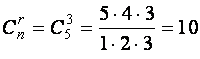 . Фактическое число различных базисных решений может
оказаться меньше 10.
. Фактическое число различных базисных решений может
оказаться меньше 10.
Так
как число свободных неизвестных два (меньше числа ![]() = 3 базисных неизвестных и потому за ними легче следить!), то
всевозможные группы неизвестных по два (сочетания из пяти по два, а их также
10), которые могут оказаться свободными, будут следующие:
= 3 базисных неизвестных и потому за ними легче следить!), то
всевозможные группы неизвестных по два (сочетания из пяти по два, а их также
10), которые могут оказаться свободными, будут следующие: ![]()
![]()
![]() .
.
Будем
строить последовательность преобразований так, чтобы в определенном порядке
перебрать все эти группировки неизвестных.
В
исходной таблице свободными неизвестными являются ![]() и
и ![]() (им соответствуют
неединичные столбцы коэффициентов
(им соответствуют
неединичные столбцы коэффициентов ![]() и
и ![]() ) .
) .
Этой
приведенной системе, как уже отмечалось, соответствует базисное решение ![]() . Выбрав ключевым элементом
. Выбрав ключевым элементом ![]() (при этом уже здесь и
в последующих итерациях мы не выделяем ключевую строку и ключевой столбец в
целях большей "прозрачности" таблицы) и переходя к следующей матрице,
получаем на I итерации
новую пару свободных неизвестных
(при этом уже здесь и
в последующих итерациях мы не выделяем ключевую строку и ключевой столбец в
целях большей "прозрачности" таблицы) и переходя к следующей матрице,
получаем на I итерации
новую пару свободных неизвестных ![]() и
и ![]() и
соответствующее базисное решение
и
соответствующее базисное решение ![]() .
.
Далее,
выбрав в качестве ключевого элемента ![]() , переходим на II итерации к
базисному решению
, переходим на II итерации к
базисному решению ![]() , связанному со свободными неизвестными
, связанному со свободными неизвестными ![]() ,
, ![]() , и т.д.
, и т.д.
Таблица 9
|
№ итерации |
i |
Базис |
|
|
|
|
|
|
|
Базисное решение |
|
Исходная система |
1 |
|
1 |
1 |
0 |
0 |
-3 |
2 |
1 |
|
|
2 |
|
3 |
0 |
0 |
1 |
1 |
1 |
6 |
||
|
3 |
|
0 |
0 |
1 |
0 |
-2 |
3 |
2 |
||
|
I |
1 |
|
1 |
1 |
0 |
0 |
-3 |
2 |
1 |
|
|
2 |
|
0 |
-3 |
0 |
1 |
10 |
-5 |
3 |
||
|
3 |
|
0 |
0 |
1 |
0 |
-2 |
3 |
2 |
||
|
II |
1 |
|
1 |
0 |
0 |
|
|
|
2 |
|
|
2 |
|
0 |
1 |
0 |
- |
- |
|
-1 |
||
|
3 |
|
0 |
0 |
1 |
0 |
-2 |
3 |
2 |
||
|
III |
1 |
|
3 |
0 |
0 |
1 |
1 |
1 |
6 |
|
|
2 |
|
10 |
1 |
0 |
3 |
0 |
5 |
19 |
||
|
3 |
|
6 |
0 |
1 |
2 |
0 |
5 |
14 |
||
|
IV |
1 |
|
0 |
- |
0 |
|
1 |
- |
|
|
|
2 |
|
1 |
|
0 |
|
0 |
|
|
||
|
3 |
|
0 |
- |
1 |
|
0 |
2 |
|
|
V |
1 |
|
0 |
0 |
- |
0 |
1 |
- |
-1 |
|
|
2 |
|
1 |
0 |
|
|
0 |
|
|
||
|
3 |
|
0 |
1 |
- |
- |
0 |
- |
- |
||
|
VI |
1 |
|
0 |
0 |
- |
0 |
1 |
- |
-1 |
|
|
2 |
|
3 |
0 |
|
1 |
0 |
|
7 |
||
|
3 |
|
1 |
1 |
- |
0 |
0 |
- |
-2 |
||
|
VII |
1 |
|
0 |
0 |
- |
0 |
1 |
- |
-1 |
|
|
2 |
|
0 |
-3 |
5 |
1 |
0 |
10 |
13 |
||
|
3 |
|
1 |
1 |
- |
0 |
0 |
- |
-2 |
||
|
VIII |
1 |
|
- |
- |
0 |
0 |
1 |
- |
- |
|
|
2 |
|
|
|
0 |
1 |
0 |
|
|
||
|
3 |
|
- |
- |
1 |
0 |
0 |
|
|
На VIII итерации
преобразования заканчиваются, так как единственная неиспользованная комбинация свободных неизвестных ![]() и
и ![]() (уже найдены 9 из 10
возможных базисных решений) не может быть получена. В самом
деле, при этом базисными неизвестными были бы
(уже найдены 9 из 10
возможных базисных решений) не может быть получена. В самом
деле, при этом базисными неизвестными были бы
![]() ,
, ![]() и
и ![]() . Удобнее всего было бы воспользоваться II итерацией, в которой
базисные неизвестные
. Удобнее всего было бы воспользоваться II итерацией, в которой
базисные неизвестные ![]() ,
, ![]() и
и ![]() , и поэтому достаточно
ввести в базис
, и поэтому достаточно
ввести в базис ![]() вместо
вместо ![]() .
.
Но
в этой таблице элемент ![]() , и он не может быть взят в качестве ключевого.
, и он не может быть взят в качестве ключевого.
Итак,
данная система имеет только 9 базисных решений (меньше 10).
Истинная
(глубинная) причина этого факта состоит в следующем. Если столбцы коэффициентов
при неизвестных ![]() ,
, ![]() и
и ![]() в исходной системе
записать в виде векторов (в строку)
в исходной системе
записать в виде векторов (в строку) ![]() и составить из них
линейную комбинацию
и составить из них
линейную комбинацию ![]() (среди коэффициентов
которой есть ненулевые), то получим нулевой вектор
(среди коэффициентов
которой есть ненулевые), то получим нулевой вектор ![]() , все координаты которого равны нулю. Это означает, что
векторы
, все координаты которого равны нулю. Это означает, что
векторы ![]() и
и ![]() линейно зависимы и поэтому не могут служить базисом системы
векторов–коэффициентов.
линейно зависимы и поэтому не могут служить базисом системы
векторов–коэффициентов.
Напомним,
что система векторов ![]() называется линейно зависимой, если равенство
называется линейно зависимой, если равенство
|
|
(8) |
где ![]() - числа, выполняется
для некоторого набора этих чисел, в котором есть хотя бы одно число, отличное от нуля.
- числа, выполняется
для некоторого набора этих чисел, в котором есть хотя бы одно число, отличное от нуля.
Линейно независимой
система называется в противном случае, т.е. если равенство (8) выполняется только при ![]() .
.
Обратим внимание, что при ![]() равенство (8)
выполняется для любых
равенство (8)
выполняется для любых ![]() векторов.
векторов.
Заметим, что единичные векторы в любом допустимом количестве линейно независимы.
Например, векторы ![]() линейно независимы,
так как из векторного равенства
линейно независимы,
так как из векторного равенства ![]()
следует 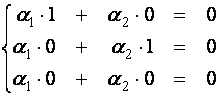 , откуда
, откуда
![]() .
.
Читатель легко проверит линейную независимость
векторов ![]()
![]() (это векторы
единичного базиса II
итерации таблицы Гаусса 9).
(это векторы
единичного базиса II
итерации таблицы Гаусса 9).