Метод Жордана-Гаусса

Еще раз обратим внимание, что в методе Гаусса в процессе преобразования расширенной матрицы системы к ступенчатому виду идет последовательное движение по строкам сверху вниз; затем по ступенчатой матрице составляется новая система, равносильная исходной, из которой последовательным движением снизу вверх находятся значения неизвестных (если система определенная) или выражения базисных неизвестных через свободные (если система неопределенная).

При этом в процессе преобразований базисные неизвестные исключаются только из всех последующих уравнений.

Метод Жордана-Гаусса отличается тем, что каждая базисная неизвестная исключается из всех уравнений, кроме одного, т.е. не только из всех последующих уравнений, но и всех предыдущих.

Продемонстрируем это на примерах.

Пример 1. Решите методом Жордана-Гаусса систему линейных уравнений

.

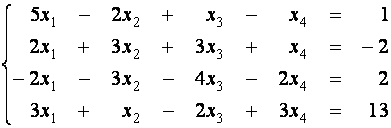Решение.

Выпишем расширенную матрицу системы и будем проводить элементарные преобразования ее строк методом Жордана-Гаусса.

~~

~ ~ ~

~ ~ ~

~ ~ ~

~ ~ .

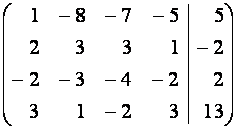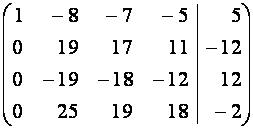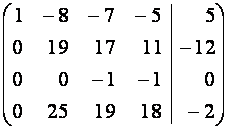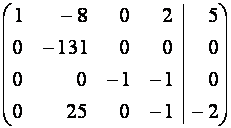
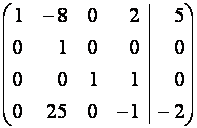Матрица приведена к ступенчатому виду , ее ранг равен 4. Одновременно к ступенчатому виду приведена и матрица системы :

.

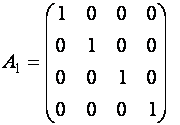Ее ранг также равен 4. Следовательно, система совместна (по теореме Кронекера-Капелли). И так как число неизвестных 4 равно рангу системы, то система определенная (имеет единственное решение). Все неизвестные базисные. Система, соответствующая матрице , имеет вид:

.

(*)

В каждом уравнении одна (базисная) неизвестная.

Решение системы .

Заметим, что матрица имеет диагональный вид; более того, она единичная.

Ее вектор-столбцы (и вектор-строки) называются единичными векторами

Про систему уравнений вида (*) принято говорить, что она приведена к единичному базису .

Пример 2. Методом Жордана-Гаусса решите систему линейных уравнений:

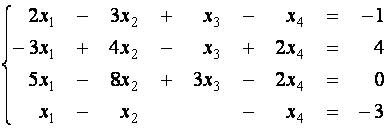
Решение.

~ ~

~ ~ ~

~ .

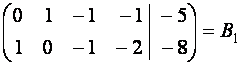Запишем систему, соответствующую матрице :

.

(**)

Базисные неизвестные - и ; остальные и - свободные. Общее решение системы имеет вид

.

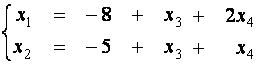Базисное решение системы: = = 0, = -8, = -5,

В нем свободные неизвестные равны нулю, а базисные равны свободным членам системы (**).

Заметим, что система (**) приведена к единичному базису 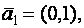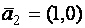с базисными неизвестным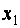и и .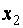

Возникает вопрос: можно ли взять другие неизвестные в качестве базисных и получить новое базисное решение? Для ответа на него продолжим элементарные преобразования матрицы :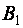

~ ~

~ .

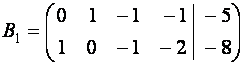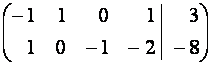
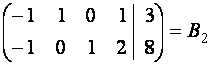Матрице соответствует система

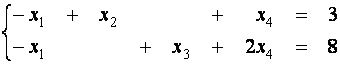
или

(***)

с базисными неизвестными и и свободными неизвестными и .

Система (***) приведена к единичному базису .

При этом одно базисное неизвестное 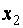сохранилось, а второе (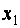) заменилось на 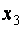. Принято в этом случае говорить, что система (***) получена из системы (**) путем однократного замещения переменных (неизвестных).

Новое общее решение исходной системы имеет вид:

,

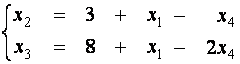а новое базисное решение

А сколько еще (других) базисных решений можно получить?

Так как число базисных неизвестных равно рангу системы, а число всех неизвестных равно , то число различных наборов по переменных из переменных равно числу сочетаний из элементов по элементов.

В нашем случае = 4, = 2, поэтому максимально возможное число различных базисных решений системы равно .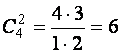

Читатель легко убедится самостоятельно, что данная система имеет именно 6 различных базисных решений. Кроме указанных это будут:

;; ;.
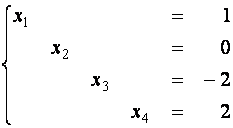
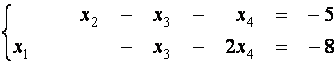