Метод Гаусса

Метод Гаусса решения систем линейных уравнений – метод последовательного исключения неизвестных – состоит в приведении этой системы с помощью элементарных преобразований к ступенчатому виду.

Удобнее всего это сделать путем приведения (с помощью элементарных преобразований строк) расширенной матрицы данной системы к ступенчатой матрице с последующей записью системы линейных уравнений, соответствующей расширенной матрице .

Полученная система равносильна исходной, так как между элементарными преобразованиями системы и элементарными преобразованиями строк ее расширенной матрицы имеет место взаимно однозначное соответствие, а при элементарных преобразованиях системы она переходит в равносильную.

Пример 1. Матрица

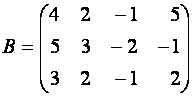
является расширенной матрицей системы

,

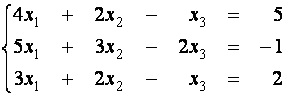так как ее можно записать в виде

,

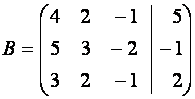и она может быть приведена к ступенчатому виду :

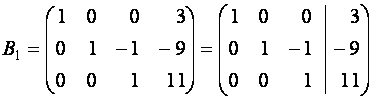
Матрице соответствует ступенчатая система линейных уравнений (равносильная исходной)

,

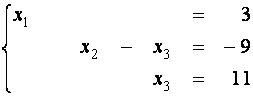из которой, двигаясь снизу вверх, т.е. от третьего уравнения к первому, последовательно находим

Таким образом, решение исходной системы существует единственно и имеет вид .

Замечание 1. При приведении к ступенчатому виду матрицы (расширенной матрицы системы) одновременно матрица системы

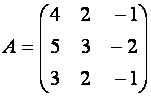
была приведена к ступенчатому виду

Замечание 2. Число строк матрицы равно числу строк матрицы и равно числу неизвестных в системе.

Пример 2. Решите систему линейных уравнений методом Гаусса:

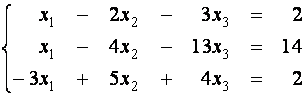
Решение

Выпишем расширенную матрицу данной системы и приведем ее к ступенчатому виду.

~ ~

~ ~ .

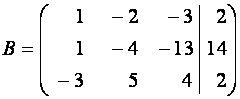
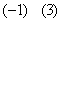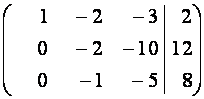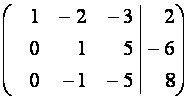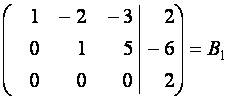Пользуясь матрицей , запишем систему уравнений, равносильную заданной:

.

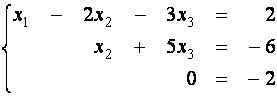Эта система несовместна, так как последнее уравнение не выполняется ни при каких значениях . Значит, и исходная система несовместна (Почему?).

Заметим, что для данной системы ступенчатая матрица имеет три строки, а ступенчатая матрица 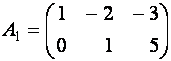- только две (нулевая строка вычеркнута).

Пример 3. Решите систему линейных уравнений методом Гаусса:

.

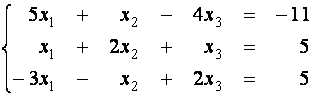Решение.

Как и в предыдущем примере

~ ~

~ ~ ~

~ ~ .

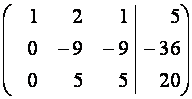
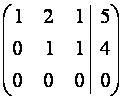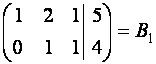Заметим, что в этом примере матрица

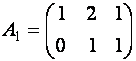
имеет две строки, как и матрица , но это число меньше трех – числа неизвестных.

Матрице соответствует ступенчатая система

,

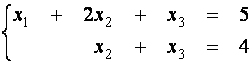содержащая два уравнения с тремя неизвестными.

В этом случае (когда число уравнений меньше числа неизвестных) принято неизвестные, с которых начинаются уравнения ступенчатой системы (а в нашем случае это и ) называть главными, или базисными, а остальные (в нашем случае это ) – свободными. Возьмем для свободной неизвестной какое-либо (произвольное) числовое значение, например, =1. Тогда, поднимаясь по ступенчатой системе снизу вверх (как и в примере 3), получим однозначно определенные значения главных неизвестных:

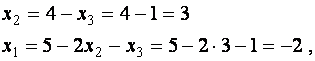
а вместе с ними и решение системы .

Взяв = 2, мы получим другое решение системы .

Таким образом, ступенчатая система, а вместе с ней и исходная, являются неопределенными.

Так как для свободной неизвестной различные значения можно выбрать бесконечным числом способов, то при этом получается бесконечное множество решений системы.

Выразим базисные неизвестные через свободные неизвестные (и свободные члены):

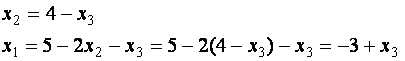
или

.

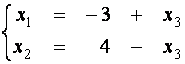Полученную систему уравнений (выражающую главные неизвестные через свободные) будем называть общим решением исходной системы.

Решение системы, полученное из общего решения при определенных значениях свободных переменных, будем называть частным решением.

Частное решение, соответствующее нулевым значениям свободных переменных, назовем базисным решением системы.

Таким образом, для заданной системы общее решение имеет вид

,

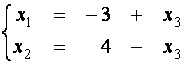частными решениями являются, например, решения , , базисным решением является Заметим, что в базисном решении все свободные переменные равны нулю, а базисные - соответствующим свободным членам в записи общего решения.

Пример 4. Решите систему линейных уравнений.

.

Решение.

~ ~

~ ~ ~

~ ~ ;

.

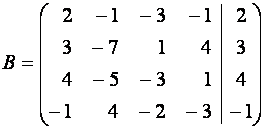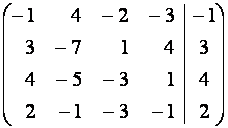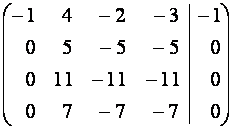
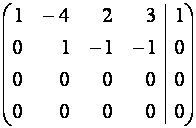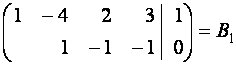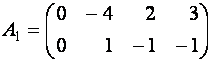Матрицы и содержат одинаковое число строк – две, но это меньше числа неизвестных в системе – четырех.

Выписываем ступенчатую систему по матрице :

.

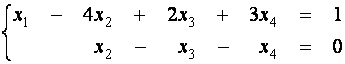Здесь и - базисные неизвестные, и - свободные неизвестные.

Находим общее решение системы:

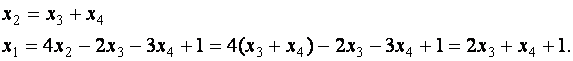
Итак, общее решение системы

.

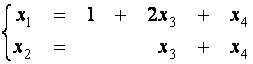Базисное решение системы: (при ) .

Анализируя примеры 3-6, замечаем, что система линейных уравнений может быть совместной или несовместной, а в случае совместности – определенной (т.е. иметь единственное решение) или неопределенной (иметь бесконечное множество решений).

Более того, из процесса решения систем в этих примерах следуют простые признаки перечисленных случаев.

1. Система совместна тогда и только тогда, когда число строк в ступенчатой матрице совпадает с числом строк в ступенчатой матрице .

2. В случае совместности система тогда и только тогда является определенной, когда число строк матрицы равно числу неизвестных системы.

Число строк ступенчатой матрицы (или ) принято называть рангом матрицы (или ).

Вообще, рангом произвольной матрицы называют число строк (столбцов) ступенчатой матрицы , полученной из матрицы с помощью элементарных преобразований ее строк (столбцов).

Теперь утверждения 1-2 можно переформулировать следующим образом.

Ø 1. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы.

Ø 2. В случае совместности система тогда и только тогда является определенной, когда ранг матрицы системы равен числу ее неизвестных.

Заметим, что в такой формулировке утверждение 1 представляет собой известную теорему Кронекера-Капелли, связанную с именами итальянского математика Альфреда Капелли (1855-1910) и немецкого математика Леопольда Кронекера (1823-1891).