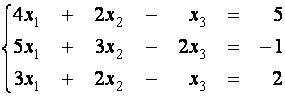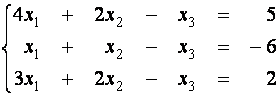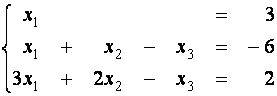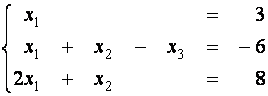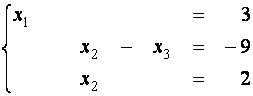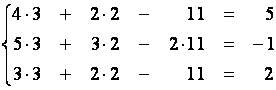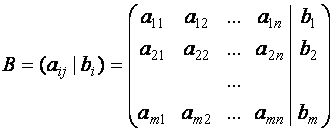Основные понятия
Система m
линейных уравнений с n
неизвестными ![]() имеет вид
имеет вид
|
|
(1) |
Каждое уравнение системы можно записать в более компактной форме
|
|
|
где ![]() - знак
суммирования,
- знак
суммирования, ![]() - коэффициент в
- коэффициент в ![]() - ом уравнении при неизвестной
- ом уравнении при неизвестной ![]() ,
, ![]() - свободный член
- свободный член ![]() - ого уравнения; при этом
- ого уравнения; при этом
![]() изменяется от 1 до
изменяется от 1 до ![]() , а
, а ![]() - от 1 до
- от 1 до ![]() .
.
Упорядоченная
совокупность ![]() чисел
чисел ![]() , которые при подстановке вместо неизвестных
, которые при подстановке вместо неизвестных ![]() обращают каждое из
уравнений системы (1) в верное числовое равенство, называется решением системы (1).
обращают каждое из
уравнений системы (1) в верное числовое равенство, называется решением системы (1).
Другими
словами: решением системы (1) является некоторый вектор ![]() .
.
Система
линейных уравнений, имеющая хотя бы одно решение, называется совместной, не имеющая ни одного решения,
называется несовместной.
Совместная
система линейных уравнений называется определенной,
если она имеет единственное решение, и неопределенной, если она имеет
более одного решения.
Две
системы линейных уравнений с одними и теми же неизвестными называются равносильными, или эквивалентными, если каждое
решение одной системы является решением другой системы, и наоборот (или если
обе системы несовместны).
Элементарными преобразованиями системы
(1) будем называть преобразования вида:
1.
Перестановка
любых двух уравнений;
2.
Умножение какого-либо уравнения на число, отличное от
нуля;
3.
Прибавление к обеим частям одного уравнения
соответствующих частей другого уравнения, умноженных на одно и то же число,
отличное от нуля;
4.
Отбрасывание уравнения, все коэффициенты которого и
свободный член равны нулю.
Справедливо
следующее утверждение.
Ø
При элементарных преобразованиях система (1) переходит
в равносильную ей систему.
Приведем
пример решения системы линейных уравнений с помощью элементарных
преобразований.
Пример 1. Решите с помощью элементарных преобразований
следующую систему линейных уравнений
|
|
|
Решение.
Будем
использовать для обозначения эквивалентности
систем уравнений знак Û.
|
|
|
Û |
(первое
уравнение умножим на (-1) и прибавим ко второму) |
|
Û |
|
Û |
(третье
уравнение умножим на (-1) и прибавим к первому) |
|
Û |
|
Û |
(второе
уравнение умножим на (-1) и прибавим к третьему) |
|
Û |
|
Û |
(первое
уравнение умножим на (-1) и прибавим ко второму, а затем умножим его же на
(-2) и прибавим к третьему) |
|
Û |
|
Û |
(третье
уравнение умножим на (-1) и прибавим ко второму) |
|
Û |
|
Û |
(второе
уравнение умножим на (-1) и после
этого переставим с третьим) |
|
Û |
|
|
|
Мы
привели исходную систему к виду, разрешенному относительно неизвестных, откуда ![]() .
.
Сделаем
проверку:
|
|
|
Получили
три верные числовые равенства.
Итак,
искомое решение ![]() , то есть исходная система оказалась совместной и
определенной.
, то есть исходная система оказалась совместной и
определенной.
Анализируя
процесс решения системы, сделаем несколько наблюдений.
1.
В каждом уравнении преобразованной системы содержится
ровно одна неизвестная (а остальные исключены), но четкого плана ее получения
не видно.
2.
Преобразованная система содержит 3 уравнения – столько
же, сколько и исходная. Технически это понятно, так как использовались только
три первые из элементарных преобразований, а четвертое применять не потребовалось.
3.
В процессе преобразований уравнений системы фактически
изменялись только ее коэффициенты и свободные члены.
Метод
последовательного исключения неизвестных принадлежит великому немецкому
математику Карлу Фридриху Гауссу (1777-1855) и, естественно, носит его имя.
Этот
метод был усовершенствован известным французским математиком Камилем Мари Эдмоном Жорданом (1838-1922) и в новом виде стал называться методом
Жордана-Гаусса.
Мы
рассмотрим последовательно оба метода: метод Гаусса и метод Жордана-Гаусса.
В
плане использования третьего наблюдения введем понятие матрицы.
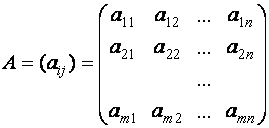
Матрицей размера ![]() будем называть
прямоугольную таблицу, состоящую из чисел и имеющую
будем называть
прямоугольную таблицу, состоящую из чисел и имеющую ![]() строк и
строк и ![]() столбцов.
столбцов.
Числа,
входящие в матрицу, принято называть ее элементами
и обозначать ![]() , где индекс
, где индекс ![]() означает номер строки, а индекс
означает номер строки, а индекс ![]() - номер столбца
матрицы, на пересечении которых стоит данный
элемент
- номер столбца
матрицы, на пересечении которых стоит данный
элемент ![]() .
.
Сама
матрица сокращенно обозначается символом ![]() или просто заглавной
буквой:
или просто заглавной
буквой:
|
|
(2) |
При
этом ![]() -ая строка состоит из
элементов
-ая строка состоит из
элементов ![]() , а
, а ![]() - ый
столбец – из элементов
- ый
столбец – из элементов ![]() . При
. При ![]() матрицу будет называть
квадратной порядка
матрицу будет называть
квадратной порядка ![]() . Для квадратной матрицы вводится понятие главной диагонали, состоящей из
элементов
. Для квадратной матрицы вводится понятие главной диагонали, состоящей из
элементов ![]() .
.
Матрица
![]() , у которой все элементы вне главной диагонали равны нулю,
называется диагональной, а в случае
, у которой все элементы вне главной диагонали равны нулю,
называется диагональной, а в случае ![]() - скалярной матрицей.
- скалярной матрицей.
Скалярная
матрица при ![]() называется единичной и обозначается
называется единичной и обозначается ![]() или просто
или просто ![]() (когда порядок матрицы
фиксирован).
(когда порядок матрицы
фиксирован).
Треугольной будем
называть квадратную матрицу, все элементы которой ниже (или выше) главной диагонали равны нулю.
Ступенчатой матрицей
назовем матрицу, в которой каждая строка, кроме первой, начинается с нулей,
причем их число возрастает с ростом номера строки, но последняя строка содержит по крайней мере один ненулевой элемент.
Примерами
ступенчатой матрицы могут служить матрицы
 ,
, 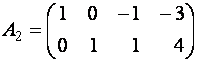 ,
,
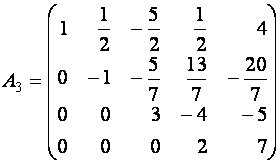 ,
,  .
.
Заметим,
что треугольная матрица является частным случаем ступенчатой. Примером треугольной матрицы служит матрица ![]() .
.
Теперь
мы можем установить соответствие между
системами линейных уравнений и матрицами.
Для
каждой системы (1) ![]() линейных уравнений с
линейных уравнений с ![]() неизвестными можно составить
матрицу
неизвестными можно составить
матрицу ![]() из коэффициентов этой
системы
из коэффициентов этой
системы
|
|
(2) |
и матрицу ![]() из коэффициентов
системы и ее свободных членов
из коэффициентов
системы и ее свободных членов ![]() :
:
|
|
(3) |
Таким
образом, матрица ![]() отличается от матрицы
отличается от матрицы ![]() наличием еще одного (
наличием еще одного (![]() - ого) столбца – столбца свободных членов.
- ого) столбца – столбца свободных членов.
Матрицу
![]() принято называть матрицей системы (1), а матрицу
принято называть матрицей системы (1), а матрицу ![]() - расширенной матрицей системы.
- расширенной матрицей системы.
С
другой стороны, имея матрицу ![]() , всегда можно записать соответствующую систему линейных
уравнений (1).
, всегда можно записать соответствующую систему линейных
уравнений (1).
В
полной аналогии с элементарными
преобразованиями системы линейных уравнений введем элементарные
преобразования строк матрицы:
1.
Перестановка любых двух строк;
2.
Умножение любой строки на число, отличное от нуля;
3.
Прибавление к одной строке другой строки, умноженной
на число, отличное от нуля;
4.
Выбрасывание нулевой строки.
Если
матрица ![]() получена из матрицы
получена из матрицы ![]() с помощью одного или
нескольких (цепочки) элементарных преобразований, то такие матрицы принято
называть эквивалентными и обозначать
этот факт
с помощью одного или
нескольких (цепочки) элементарных преобразований, то такие матрицы принято
называть эквивалентными и обозначать
этот факт ![]() .
.
С
помощью элементарных преобразований строк любую (ненулевую) матрицу можно
привести к ступенчатому (в частности, треугольному) виду.
Покажем
это на примере.
Пример 2. Приведите к
ступенчатому виду матрицу
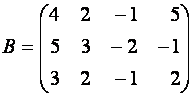
Решение.
Матрица ![]() является
целочисленной, т.е. все ее элементы целые числа. В первом столбце нет
элементов ±1 (а именно
такие элементы очень удобны для элементарных преобразований, что будет видно из
дальнейшего).
является
целочисленной, т.е. все ее элементы целые числа. В первом столбце нет
элементов ±1 (а именно
такие элементы очень удобны для элементарных преобразований, что будет видно из
дальнейшего).
Можно
было бы первую строку умножить на 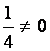 , создавая
, создавая ![]() на месте элемента
на месте элемента ![]() , но это приведет к потере целочисленности
матрицы и поэтому к относительно неудобным последующим вычислениям.
, но это приведет к потере целочисленности
матрицы и поэтому к относительно неудобным последующим вычислениям.
Поступим
иначе: умножим третью строку на ![]() и прибавим к первой,
тогда
и прибавим к первой,
тогда
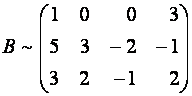
Теперь
(для создания нулей в первом столбце) умножим первую строку новой матрицы на ![]() и прибавим ко второй, а после
умножения ее же на
и прибавим ко второй, а после
умножения ее же на ![]() прибавим к третьей
строке.
прибавим к третьей
строке.
Получим
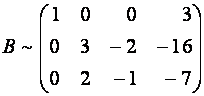
Умножим третью строку полученной матрицы на ![]() и прибавим ко второй:
и прибавим ко второй:

Умножим вторую строку на ![]() и прибавим к третьей:
и прибавим к третьей:

Матрица
![]() - ступенчатая.
- ступенчатая.
Цепочку
преобразований матрицы ![]() к ступенчатой матрице
к ступенчатой матрице ![]() можно записать
следующим образом:
можно записать
следующим образом:
![]()

![]()
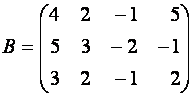
![]()
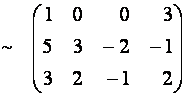
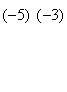 ~
~
![]()
![]()
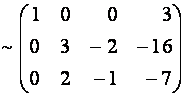
![]()

![]() ~
~
 .
.
Замечание. Можно ввести понятие элементарных преобразований и
для столбцов матрицы.
 .
.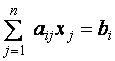 ,
,